Nghiên cứu này tiến hành thực nghiệm trên chuỗi dữ liệu thực tế là xuất khẩu gạo của Việt Nam bằng cách ước lượng mô hình AR – ARCH theo cả hai phương pháp là hồi quy OLS và hồi quy LASSO cho thấy, hồi quy LASSO phù hợp với xu hướng hiện nay là không dùng P-value và là một phương pháp thay thế hiệu quả cho hồi quy OLS trong dự báo chuỗi thời gian.

Giới thiệu

Hiện nay, ngày càng có nhiều quốc gia đang phát triển đang đi theo chiến lược công nghiệp hóa hướng vào xuất khẩu. Việc thực hiện chiến lược này nhằm mang lại một nền kinh tế tiên tiến, phồn thịnh với các chỉ tiêu kinh tế vĩ mô hiệu quả như GDP, FDI, tỷ giá hối đoái, xuất khẩu đồng thời nâng cao chất lượng cuộc sống của người dân. Để đạt được các chỉ tiêu kinh tế và mục tiêu tăng trưởng đã đề ra thì chính phủ các nước cần phải thúc đẩy xuất khẩu và đồng thời kêu gọi các nhà đầu tư nước ngoài.

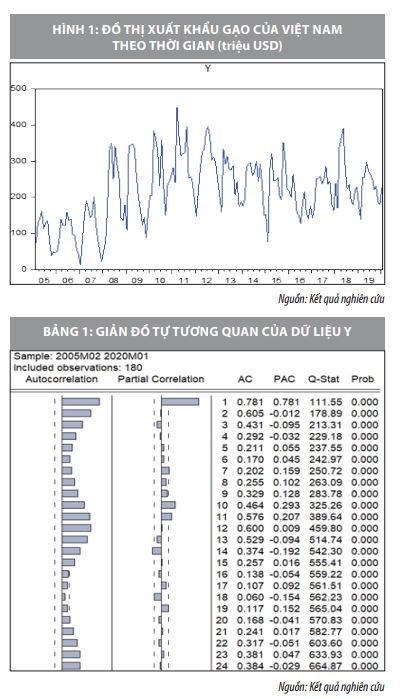
Tại Việt Nam, gạo là một trong 10 mặt hàng xuất khẩu chủ lực, đóng góp đáng kể trong tổng kim ngạch xuất khẩu của nước ta. Do đó, dự báo tình hình xuất khẩu gạo cũng như biến động của xuất khẩu gạo đóng một vai trò quan trọng giúp các doanh nghiệp, cũng như Chính phủ có những giải pháp ứng phó kịp thời để nắm bắt cơ hội phát triển hay đối phó với những khó khăn sắp tới.

Đối với dữ liệu chuỗi thời gian, sự thay đổi trong hiện tại và tương lai có thể được dự báo thông qua những hoạt động trong quá khứ. Một số mô hình nghiên cứu trong dự báo được sử dụng như mô hình san mũ, mô hình phân tích, mô hình ARIMA (Hanke, J. E., Reitsch, A. G., & Wichern, D. W. , 2001)… Trong ứng dụng, mỗi mô hình có những điểm mạnh và điểm yếu riêng và việc lựa chọn mô hình phù hợp hoàn toàn dựa vào mục đích nghiên cứu cũng như tầm quan trọng của các yếu tố cần lựa chọn. Đặc biệt, trong các mô hình cổ điển với chuỗi thời gian dừng luôn giả định rằng dữ liệu là sự hỗn hợp giữa các quá trình tự hồi quy và các quá trình trung bình trượt, hay còn gọi là mô hình ARMA (Brockwell, P. J., Davis, R. A., & Fienberg, S. E. , 1991). Thông thường, cả việc ước lượng và lựa chọn mô hình đều dựa trên giả định là các tham số không đổi và không gian các tham số có chiều thấp.

Trong thời đại dữ liệu lớn hiện nay, số lượng biến tăng lên nhanh chóng, rất khó để xác định một chuỗi dữ liệu có thực sự là một một quá trình ARMA hay không. Thay vào đó, người ta thường giả định dữ liệu được cho là một chuỗi thời gian tuyến tính, có thể được biểu diễn bằng một quá trình tự hồi quy với bậc vô hạn. Một số nghiên cứu đã được thực hiện cho thấy tính chính xác của các quá trình xấp xỉ AR (Shibata, 1980), (Goldenshluger, A., & Zeevi, A., 2001) và (Ing, C. K., & Wei, C. Z., 2005)).

Bên cạnh đó, các thuật toán thu nhỏ có tầm quan trọng lớn trong hầu hết mọi lĩnh vực thống kê do tác động ngày càng tăng của dữ liệu lớn. Đặc biệt, trong phân tích chuỗi thời gian, một kỹ thuật thu nhỏ mang lại ước lượng hiệu quả và nhanh chóng đang được sử dụng rộng rãi là hồi quy LASSO. Hồi quy LASSO được sử dụng rộng rãi bởi hai ưu điểm như sau: Thứ nhất, mô hình này có kết quả dự báo chính xác hơn so với hồi quy OLS (căn cứ vào RMSE); Thứ hai, là tính nhanh chóng và tính không phụ thuộc vào P-value trong quá trình xác định các tham số khác không của LASSO. Bài viết này thảo luận về hồi quy LASSO là một công cụ thống kê để thu được các giải pháp cho các vấn đề hồi quy như ước lượng tham số, lựa chọn mô hình và thực hiện dự báo cho chuỗi thời gian.

Phần ứng dụng, nhóm tác giả ước lượng mô hình tự hồi quy AR theo cả hai phương pháp là hồi quy OLS và hồi quy LASSO, sau đó tiến hành dự báo và so sánh hiệu quả dự báo của hai mô hình dựa trên sai số dự báo RMSE. Khi thực hiện hồi quy LASSO cho mô hình tự hồi quy, chúng tôi sử dụng một sự kết hợp được xem như một khung tiệm cận kép (Nardi, Y., & Rinaldo, A., 2011). Khung tiệm cận kép này cho phép chúng ta coi bậc tự hồi quy là gần như vô hạn. Chuỗi thời gian tự hồi quy AR với sự gia tăng của số lượng các tham số là trung gian giữa chuỗi thời gian AR có bậc tự hồi quy cố định và chuỗi thời gian AR có bậc tự hồi quy vô hạn. Sau đó, chúng tôi tiến hành xem xét phần dư của mô hình AR để xác định hiệu ứng ARCH và thực hiện ước lượng mô hình ARCH theo cả hai phương pháp OLS và LASSO. Cuối cùng chúng tôi tiến hành đánh giá hiệu quả của phương pháp hồi quy LASSO và dự báo. 

Mô hình hồi quy OLS và LASSO

Mô hình OLS cổ điển

Mô hình hồi quy tuyến tính tổng quát:

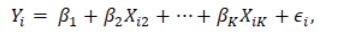
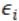
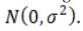
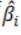
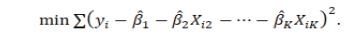
Trong đó  là nhiễu, tuân theo phân phối chuẩn Các tham số ước lượng   của mô hình theo phương pháp bình phương cực tiểu các sai số:

Các tham số ước lượng được ước lượng thỏa mãn định lý Gauss-Markov về phương sai của các sai số ước lượng là nhỏ nhất trong số các ước lượng tuyến tính và không chệch, trong đó:

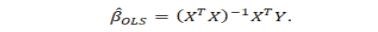
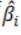
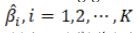
Tuy nhiên, nếu có hiện tượng đa cộng tuyến xảy ra thì việc xác định  là không thể hoặc không chính xác. Mặc dù, một ưu điểm đáng ghi nhận của hồi quy OLS là nghiệmlà xác định và duy nhất, nhưng sẽ không thể kết luận được gì nếu không ước lượng được các hệ số hồi quy. Hơn nữa, trong trường hợp thu thập được ít dữ liệu nhưng mỗi quan sát lại có nhiều thông tin cung cấp thì cũng xảy ra tình trạng khó khăn trong ước lượng các hệ số hồi quy.

Mô hình LASSO

Hồi quy LASSO là cũng phương pháp hồi quy tuyến tính đa biến có hiệu chỉnh, trong đó các tham số ước lượng được dựa vào cực tiểu của biểu thức (Owen, 2007):

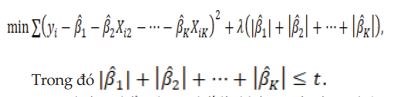
Tuy nhiên, điểm hạn chế là không có công thức nghiệm cụ thể cho bài toán này. Trong đó, hồi quy LASSO phụ thuộc vào tham số thu nhỏ  để xác định các hệ số nào sẽ có giá trị bằng không, cách xác định tham số  thông qua về mối quan hệ giữa  và  thông qua thuật toán LARS (Efron, B., Hastie, T., Johnstone, I., & Tibshirani, R., 2004). 

Ứng dụng bộ dữ liệu

Chúng tôi nghiên cứu các dữ liệu về xuất khẩu gạo (Y, đơn vị triệu USD) của Việt Nam (mã VEXRICEA) theo nguồn dữ liệu của Thomson-Reuters thu thập từ General Staticstics Office of Vietnam. Dữ liệu được nghiên cứu theo tháng trong khoảng thời gian từ tháng 2 năm 2005 đến tháng 1 năm 2020. Chúng tôi lần lượt xây dựng các mô hình dự báo cho biến động xuất khẩu gạo của Việt Nam, bắt đầu là mô hình tự hồi quy AR.

Đồ thị biểu diễn dữ liệu theo thời gian được trình bày trong hình 1. Dựa vào đồ thị hình 1, chúng ta nhận thấy dữ liệu có tính chu kỳ đặc biệt tăng cao ở những tháng giữa năm. Do đó, mô hình dự báo phù hợp cho bộ dữ liệu này có thể là mô hình ARIMA.

Mô hình AR theo phương pháp OLS và LASSO

Đối với mô hình AR theo phương pháp OLS, để lựa chọn mô hình chuỗi thời gian phù hợp, chúng tôi tiến hành kiểm tra tính dừng của chuỗi dữ liệu LY (log(Y)) thông qua bảng kết quả:

Kết quả kiểm định nghiệm đơn vị thấy rằng giá trị kiểm định t= - 4.764307 tương ứng với giá trị p-value=0 chứng tỏ dữ liệu LY là chuỗi dừng trong trường hợp có hệ số hằng số. Do đó, chúng tôi sử dụng chuỗi dữ liệu gốc trong mô hình ARIMA. Tiếp theo, chúng tôi xác định bậc của mô hình ARIMA thông qua giản đồ tự tương quan trong Hình 1.       

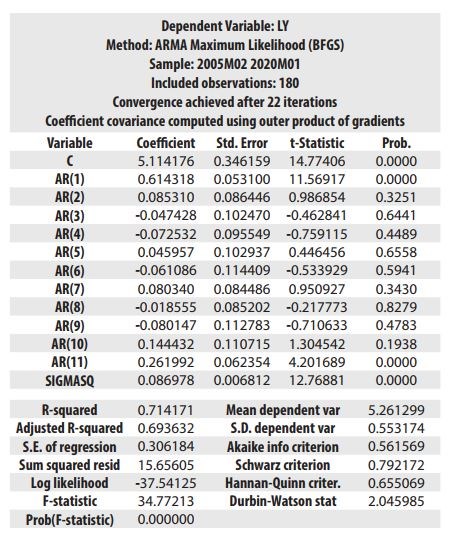
Dựa vào giản đồ tự tương quan về sự khác 0 của các hệ số tự tương quan (ACF) và tự tương quan riêng phần (PACF), chúng tôi xác định mô hình phù hợp cho chuỗi dữ liệu là mô hình tự hồi quy AR. Sau khi ước lượng mô hình AR, chúng tôi tiến hành các kiểm định và chọn mô hình AR(11) là mô hình phù hợp.

Mặc dù mô hình độ phù hợp R2=0.714 là một giá trị rất cao cộng với giá trị kiểm định độ phù hợp của mô hình là F=34.77213, tương ứng p-value=0 chứng tỏ sự phù hợp khá tốt của mô hình AR(11). Tuy nhiên việc lựa chọn được mô hình phù hợp trong trường hợp này phải thông qua một số kiểm định phức tạp.

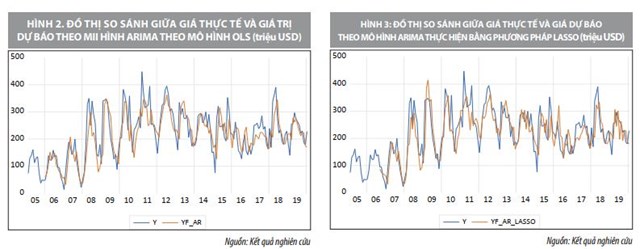
Tiếp theo, chúng tôi sẽ thực hiện dự báo bằng mô hình AR(11) và có kết quả so sánh giữa dữ liệu thực tế và dự báo được minh họa thông qua hình 2. Dựa theo đồ thị ở hình 2, chúng ta có thể thấy mô hình AR(11) được ước lượng bằng phương pháp OLS cho giá trị dự báo khá gần với giá trị thực tế với sai số dự báo RMSE bằng 55.78509.

Đối với mô hình AR theo phương pháp LASSO, bằng việc sử dụng phương pháp Yule-Walker trong việc lựa chọn bậc tự hồi quy p với p nằm trong khoảng từ 1 đến O(logn), chúng tôi thu được mô hình được chọn trong số tất cả các mô hình AR có thể có với các hệ số hồi quy tương ứng với các bậc tự hồi quy như sau:

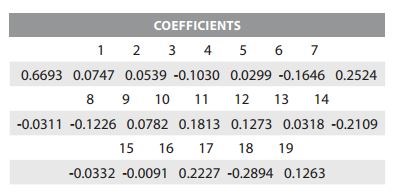
Trong kết quả trên, các giá trị đi kèm với các số thứ từ 1 đến 19 là các hệ số ước lượng của mô hình được chọn, các số thứ tự từ 1 đến 19 là các bậc từ hồi quy tương ứng của mô hình AR. Kết quả so sánh giá trị dự báo và  giá trị thực tế được minh họa qua đồ thị sau:

Đồ thị ở hình 3 cho chúng ta thấy mô hình AR được ước lượng bằng phương pháp LASSO cho giá trị dự báo rất gần với giá trị thực tế với sai số dự báo RMSE bằng 52.18894.

Mô hình ARCH theo phương pháp OLS và LASSO

Sử dụng phần dư thu được từ mô hình tự hồi quy AR(19) ở phần trước, chúng tôi tiến hành các bước kiểm định hiệu ứng ARCH của chuỗi phần dư bình phương bằng hồi quy OLS.

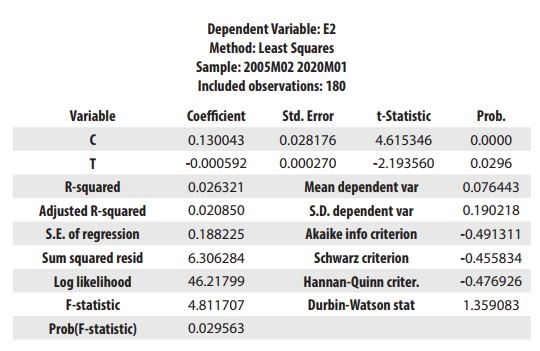
Trước tiên, chúng tôi kiểm định tính xu thế của chuỗi phần dư bình phương và thu được kết quả như sau:

Dựa vào kết quả ước lượng phần dư bình phương theo thời gian, vì P-value của các hệ số hồi quy đều nhỏ hơn 5% nên chuỗi có tính xu thế. Tiếp tục kiểm định tính dừng của chuỗi phần dư bình phương với trường hợp có hằng số và xu thế, thu được kết quả như sau:

Vì giá trị t-Statistic lớn hơn các giá trị tới hạn tại các mức ý nghĩa 1%, 5%, 10% nên ta bác bỏ H0. Vậy chuỗi phần dư bình phương là chuỗi dừng.

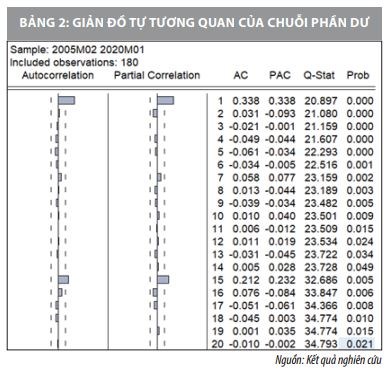
Tiếp theo, để xác định hiệu ứng ARCH, chúng tôi xem xét lược đồ ACF và PACF của chuỗi phần dư bình phương như trong hình sau:

Theo lược đồ ACF và PACF, chuỗi phần dư bình phương có hiệu ứng ARCH ở độ trễ 1 và độ trễ 15. Tiến hành các kiểm định lựa chọn mô hình, chúng tôi thu được mô hình phù hợp cho dữ liệu là mô hình ARCH(1). Kết quả ước lượng thu được là:

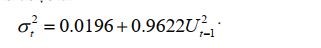
Các hệ số của mô hình ước lượng trên đều ý nghĩa ở mức 1% và mô hình ước lượng trên cho kết quả dự báo có sai số dự báo RMSE = 51.04917.

Tiếp tục ước lượng mô hình ARCH bằng phương pháp hồi quy LASSO với phương pháp Yule-Walker trong việc lựa chọn bậc tự hồi quy p của chuỗi phần dư bình phương, chúng tôi thu được kết quả là:

Coefficients: 

1
0.3379
Order selected 1 sigma^2 estimated as 0.03223

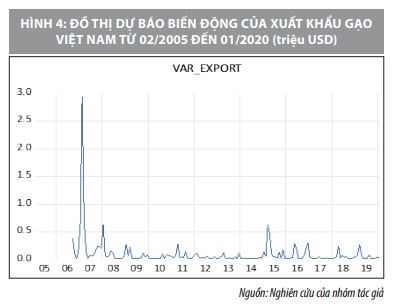
Dựa vào kết quả trên, ta thấy bằng hồi quy LASSO, bậc tự hồi quy p = 1 được chọn trong các độ trễ từ 1 đến 22. Như vậy bằng LASSO ta cũng chọn được mô hình ARCH(1) mà không phải tiến hành một số kiểm định để được kết quả cuối cùng. Đồng thời mô hình ARCH(1) bằng phương pháp hồi quy LASSO cho ta kết quả dự báo cho biến động của xuất khẩu gạo của Việt Nam với sai số dự báo RMSE = 42.8639. Kết quả dự báo cho biến động của xuất khẩu gạo được minh họa bằng đồ thị sau:

Do đó, dựa vào so sánh sai số RMSE của các mô hình ước lượng trên, mô hình ARCH(1) tiến hành bằng LASSO là mô hình được chọn để dự báo cho biến động của xuất khẩu gạo của Việt Nam. Kết quả dự báo điểm cho 6 tháng tiếp theo từ tháng 2 đến tháng 7 năm 2020 cho biến động của xuất khẩu gạo của Việt Nam là:

Kết luận

Nghiên cứu đã tiến hành dự báo biến động xuất khẩu gạo của Việt Nam bằng mô hình AR-ARCH được ước lượng theo hai phương pháp là hồi quy OLS và hồi quy LASSO. Dựa trên RMSE, nghiên cứu chỉ ra rằng, mô hình trên khi ước lượng theo phương pháp LASSO cho kết quả dự báo tốt hơn. Điều này lại một lần nữa chứng minh rằng hồi quy LASSO là một thay thế hiệu quả cho hồi quy OLS trong cả việc ước lượng hệ số hồi quy, lựa chọn mô hình và dự báo.

Qua nghiên cứu này, nhóm tác giả đã ước lượng nhằm lựa chọn các mô hình dự báo phù hợp nhất cho xuất khẩu gạo của Việt Nam theo thời gian với mục tiêu là thu được sai số dự báo nhỏ nhất có thể. Các kết quả dự báo với độ phù hợp cao chứng tỏ tính hiệu quả của các mô hình dự báo chuỗi thời gian, đưa ra triển vọng mới về các mô hình tài chính hiện đại trong áp dụng các chỉ tiêu kinh tế - xã hội. Các kết quả nghiên cứu mong muốn các giá trị dự báo trong tương lai có ý nghĩa trong việc đưa ra các chính sách phù hợp dựa trên các dự báo có ý nghĩa. 

Tài liệu tham khảo:
1. Brockwell, P. J., Davis, R. A., & Fienberg, S. E. . (1991), Time series: theory and methods. Springer Science & Business Media;
2. Efron, B., Hastie, T., Johnstone, I., & Tibshirani, R. (2004), Least angle regression;
3. The Annals of statistics, 32(2), 407-499;
4. Francq, C., & Zakoian, J. M. (2019), GARCH models: structure, statistical inference and financial applications. John Wiley & Sons;
5. Goldenshluger, A., & Zeevi, A. (2001), Nonasymptotic bounds for autoregressive time series modeling. Annals of statistics, 417-444;
6. Hanke, J. E., Reitsch, A. G., & Wichern, D. W. . (2001), Business forecasting (Vol. 9). Upper Saddle River, NJ: Prentice Hall;
7. Ing, C. K., & Wei, C. Z. (2005), Order selection for same-realization predictions in autoregressive processes. The Annals of Statistics, 33(5), 2423-2474;
8. Nardi, Y., & Rinaldo, A. (2011), Autoregressive process modeling via the lasso procedure. Journal of Multivariate Analysis, 102(3), 528-549.