Khung lý thuyết và nghiên cứu thực nghiệm

Khung lý thuyết

Tác giả nghiên cứu về biến động của thị trường chứng khoán (TTCK) và thị trường vàng Việt Nam dựa trên chỉ số VN-Index và chỉ số giá vàng theo tháng giai đoạn 2002 - 2022. Lý thuyết kinh tế giải thích cho vấn đề nghiên cứu của tác giả thuộc về mô hình định giá tài sản vốn CAPM (Capital Asset Pricing Model) được phát triển lần đầu tiên bởi William Sharpe (1964) và John Lintner (1965). Mô hình này cũng được sử dụng để xây dựng mô hình lựa chọn danh mục đầu tư của Harry Markowitz (1959). Cụ thể, danh mục đầu tư được nhà đầu tư lựa chọn tại thời điểm t-1 để tạo ra lợi nhuận khác nhau tại thời điểm sau đó là t nhằm giảm thiểu phương sai lợi nhuận và tối đa lợi nhuận được tạo ra từ Danh mục đầu tư được lựa chọn ứng với phương sai đó.

Mô hình danh mục đầu tư đưa ra các điều kiện về số học dựa trên tỷ trọng của các tài sản trong danh mục đầu tư hay danh mục đầu tư hiệu quả - phương sai - lợi nhuận trung bình.

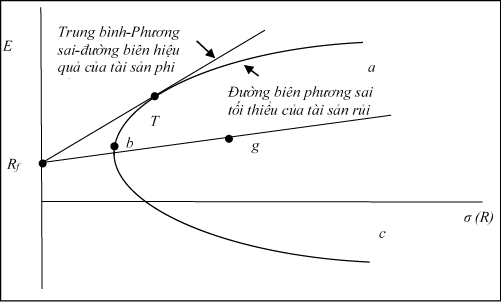
Hình 1 cho thấy, tỷ suất lợi nhuận của tài sản đầu tư là trục tung và rủi ro của tài sản đầu tư ứng với tỷ suất lợi nhuận là độ lệch chuẩn của tỷ suất lợi nhuận.Đường cong abc được gọi là đường biên phương sai tối thiểu đối với tài sản rủi ro, biểu thị cho sự kết hợp của lợi nhuận kỳ vọng và rủi ro của Danh mục đầu tư của các tài sản rủi ro nhằm giảm thiểu biến động lợi nhuận (phương sai) tương ứng với lợi nhuận kỳ vọng. Tại điểm T trên đồ thị, nhà đầu tư có thể nhận được tỷ suất lợi nhuận bằng với tỷ suất lợi nhuận tại điểm giữa hay tại điểm này tỷ suất lợi nhuận biến động thấp hơn.

Nếu tất cả vốn được đầu tư vào chứng khoán phi rủi ro thì tỷ suất lợi nhuận tương ứng đạt được tại điểm Rf mà tại đó phương sai của danh mục đầu tư là bằng 0. Tại điểm g trên Hình 1 là vốn đầu tư được phân bổ vào tài sản phi rủi ro cùng với một số danh mục đầu tư rủi ro, vì vậy đường này là đường thẳng được hình thành từ tỷ suất lợi nhuận phi rủi ro tại điểm Rf đến điểm g trên Hình 1.

Theo giả định của CAPM danh mục thị trường M phải nằm trên đường biên phương sai tối thiểu nếu thị trường tài sản ổn định. Điều này cũng có nghĩa mối quan hệ đại số đúng cho bất kỳ danh mục phương sai tối thiểu cũng sẽ đúng cho danh mục thị trường. Điều kiện phương sai tối thiểu của danh mục thị trường M với N tài sản rủi ro:

E(Ri ) = E(RZM ) + [ E(RM ) – E(RZM)] βiM , i = 1,…..N. (1)

Trong đó, E(Ri ) là tỷ suất lợi nhuận kỳ vọng của tài sản i, và βiM hệ số beta của tài sản i là hiệp phương sai của tỷ suất lợi nhuận của tài sản i với tỷ suất lợi nhuận của thị trường chia cho phương sai của tỷ suất lợi nhuận của thị trường.

(Market Beta) β_iM=(cov( R_i,R_M))/(σ^2 (R_M)) (2)

E(RZM ) là tỷ suất lợi nhuận kỳ vọng của tài sản có hệ số beta của thị trường là 0, đẳng thức thứ hai bên phải của phương trình (1) là phần bù rủi ro với hệ số beta thị trường của tài sản i, βiM, nhân cho phần bù của mỗi đơn vị beta từ chênh lệch của tỷ suất lợi nhuận kỳ vọng của thị trường E(RM) trừ cho tỷ suất lợi nhuận kỳ vọng của tài sản E(RZM) có hệ số beta của thị trường là 0.

Sharpe - Lintner đã phát triển mô hình với giả định về tài sản phi rủi ro sẽ điều chỉnh về tương ứng với tỷ suất lợi nhuận kỳ vọng của tài sản E (RZM) có hệ số beta của thị trường bằng 0. Vì vậy, khi tài sản phi rủi ro sẽ có tỷ suất lợi nhuận kỳ vọng từ tài sản sẽ không tương quan với tỷ suất lợi nhuận của thị trường và E (RZM) cũng chính là lãi suất phi rủi ro Rf. Do đó, mối quan hệ giữa tỷ suất lợi nhuận kỳ vọng và hệ số beta sẽ là phương trình CAPM Sharpe-Lintner:

(Sharpe-Lintner CAPM) E(Ri ) = (Rf ) + [E(RM ) – Rf] βiM , i =

1,….,N. (3)

Tỷ suất lợi nhuận của bất kỳ tài sản rủi ro i sẽ bằng lãi suất phi rủi ro Rf, cộng cho phần bù rủi ro tương ứng với hệ số rủi ro beta của thị trường βiM nhân cho phần bù của mỗi đơn vị rủi ro E(RM ) – Rf

Mô hình CAPM xác định lợi nhuận kỳ vọng liên quan đến hệ số beta của thị trường được áp dụng cho danh mục thị trường trong mối quan hệ giữa lợi nhuận kỳ vọng và hệ số rủi ro beta của danh mục đại diện cho bất kỳ danh mục hiệu quả - phương sai – trung bình. Hiệu quả của danh mục thị trường (Fama và French, 2004).

Vì mục tiêu nghiên cứu về các trạng thái chuyển đổi của chỉ số Vn- Index và chỉ số giá vàng hay các trạng thái biến động của chỉ số Vn - Index và chỉ số giá vàng. Tác giả cho rằng, mô hình CAPM của William Sharpe (1964) và John Lintner (1965) là mô hình phù hợp để thấy biến động của tỷ suất lợi nhuận từ đường thị trường chứng khoán (Security Market Line - SML), cũng như rủi ro từ Danh mục đầu tư của thị trường qua hệ số beta và phần bù rủi ro từ biến động của thị trường.

Nghiên cứu thực nghiệm

Các nghiên cứu trước đó để kiểm chứng mối quan hệ của tài sản tài chính, hàng hóa và bất động sản là các thành phần trong Danh mục đầu tư là những cặp đôi có mối quan hệ chuyển đổi theo từng cặp tài sản. Cụ thể như: Giá dầu thô và thị trường bất động sản, giá vàng và thị trường chứng khoán hay giá vàng và giá dầu thô, cấu trúc lãi suất và đầu tư bất động sản hay mối quan hệ kết nối của bộ ba tài sản gồm: Bất động sản, hàng hóa và tài sản tài chính.

Nghiên cứu của Chan và cộng sự (2011) cho thấy, có sự chuyển đổi trạng thái biến động lợi nhuận đầu tư giữa các tài sản tài chính là chứng khoán Mỹ, trái phiếu kho bạc, các tài sản hàng hóa là giá dầu, vàng và bất động sản. Nghiên cứu này cho thấy có sự chuyển đổi hai trạng thái là trạng thái bình ổn hay biến động thấp tương ứng với giai đoạn kinh tế mở rộng và trạng thái khủng hoảng hay biến động cao hơn. Hay với trạng thái kinh tế mở rộng (trạng thái 1) các tài sản là chứng khoán, bất động sản điều có lợi nhuận dương, nhưng với trạng thái kinh tế suy thoái (trạng thái 2) thì chứng khoán và bất động sản lại có lợi nhuận âm. Nghiên cứu này cũng cho rằng, trái phiếu chính phủ là tài sản an toàn để phòng ngừa rủi ro tài chính trong giai đoạn xảy ra khủng hoảng.

Nghiên cứu của Alola (2020) về chuyển đổi trạng thái của giá dầu thô và thị trường bất động sản tại Saudi Arabia từ ngày 03/10/2005 đến 29/03/2018 cho thấy, kết quả đạt được của giá dầu đến thị trường bất động sản đều tích cực tại cả 2 trạng thái, cũng như lợi nhuận đạt được của giá dầu thô tăng trưởng tốt hơn trong thời kỳ xảy ra khủng hoảng kinh tế dù cho giá dầu thô có biến động mạnh trong trạng thái 2. Sự bất ổn định của giá dầu trong trạng thái 2 cũng là tác động xấu đến thị trường bất động sản tại Saudi Arabia.

Nghiên cứu của Youssef và Mokni (2021) về mối quan hệ chuyển đổi của lợi nhuận từ giá dầu khí và lợi nhuận giá vàng hay tài sản trú ẩn an toàn trong thời kỳ biến động từ tác động của khủng hoảng tài chính toàn cầu và dịch bệnh COVID-19. Trong nghiên cứu này, tác giả sử dụng mô hình hồi quy phân vị để đánh giá mối quan hệ tác động từ các cú sốc của cung - cầu dầu khí tại các phân vị khác nhau của giá vàng và mô hình hồi quy phân vị chuyển tiếp trạng thái Markov để xác định các trạng thái chuyển đổi.

Kết quả nghiên cứu cho thấy, các cú sốc về cung và cầu giá dầu có tác động tích cực đến lợi nhuận của vàng và tác động này không bị ảnh hưởng bởi quy mô, dấu hiệu và mức độ từ cú sốc của cung và cầu của giá dầu. Đối với mô hình phân vị chuyển đổi trạng thái, cú sốc từ nguồn cung dầu tác động tích cực đến lợi nhuận từ vàng tại trạng thái 1 (trạng thái biến động nhẹ), nhưng tác động tiêu cực nhẹ đến giá vàng trong trạng thái 2 (trạng thái thị trường con gấu) và trạng thái 3 (trạng thái thị trường con trâu) là những trạng thái thị trường biến động mạnh.

Từ nghiên cứu thực nghiệm trên cho thấy có điểm tương đồng về kết quả là các tài sản đầu tư là hàng hóa vàng và dầu khí được xem là tài sản đầu tư an toàn trong trạng thái biến động của thị trường hay khi thị trường bị ảnh hưởng bởi suy thoái kinh tế và dịch bệnh COVID-19. Điểm khác biệt trong nghiên cứu này là tác giả nghiên cứu sự chuyển đổi đầu tư giữa vàng và chứng khoán trong điều kiện nền kinh tế Việt Nam trong giai đoạn 2002 - 2022.

Giả thuyết nghiên cứu

Theo Mô hình CAPM của Sharpe (1964) và Lintner (1965) cho thấy, lợi nhuận kỳ vọng của TTCK phụ thuộc vào phần bù từ rủi ro thị trường là chênh lệch của tài sản rủi ro so với tài sản phi rủi ro cùng với hệ số rủi ro của danh mục tài sản đầu tư beta.

Giả thuyết: Chỉ số VN- Index sẽ chuyển đổi sang trạng thái biến động mạnh tại các thời điểm khủng hoảng kinh tế và dịch bệnh và chỉ số giá vàng được xem là tài sản đầu tư an toàn trong các trạng thái biến động đó (Chkili, 2017; Youssef và cộng sự, 2021).

Phương pháp và mô hình nghiên cứu

Phương pháp nghiên cứu

Trong nghiên cứu này, tác giả sử dụng phương pháp nghiên cứu được sử dụng để xác định thời điểm chuyển đổi trạng thái của chỉ số VN - Index và chỉ số giá vàng là phương pháp hồi quy động chuyển đổi trạng thái Markov (Markov Switching Dynamics Regression - MSDR) của Hamilton (1989). Trước khi thực hiện hồi quy, tác giả kiểm định tính dừng của chuỗi thời gian dữ liệu chỉ số VN - Index và chỉ số giá vàng (Phillips và Perron, 1988) với kết quả đạt được là chuỗi của chỉ số Vnindex và chỉ số giá vàng đều dừng ở sai phân bậc 1.

Hơn nữa, sự phù hợp của mô hình chuyển đổi trạng thái của Markov (hay mô hình phi tuyến) được kiểm định cho cả một trạng thái, hai trạng thái, và ba trạng thái cảu các biến nghiên cứu là chỉ số VN - Index, chỉ số giá vàng là phi tuyến. Trạng thái phù hợp là trạng thái thứ hai với chỉ số SBIC cao hơn. Vì vậy, phương pháp hồi quy phù hợp để ước lượng trạng thái chuyển đổi là phi tuyến.

Mô hình nghiên cứu

Mô hình xác định hệ số tác động không đổi tương ứng cho các trạng thái được xác định dựa trên hồi quy động chuyển đổi trạng thái Markov của Hamilton (1989), mô hình tổng quát như sau:

Yt = µSt + εt (4)

Yt là biến đại diện cho ma trận của chỉ số Vnindex và chỉ số giá vàng tương ứng trạng thái St và µSt = (µ1St, µ2St ) là vector của chỉ số trung bình của chỉ số Vnindex và chỉ số giá vàng tại trạng thái St tương ứng với quá trình Markov trạng thái M với ma trận xác suất chuyển đổi trạng thái như sau:

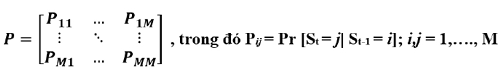
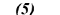
εt : là sai số ngẫu nhiên trong mô hình tương ứng với trạng thái St-. và phần dư tuân theo phân bố xác suất chuẩn tương ứng với điều kiện của trạng thái, εt ~ N(0, ∑St) với εt = (ε1t , ε2t ) là ma trận hiệp phương sai 2 x 2 tương ứng theo trạng thái St :

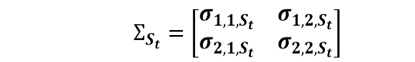(6)

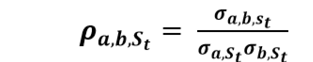(7)

và là tương quan đồng thời giữa chỉ số a và chỉ số b

Kết quả là phần phối có điều kiện của yt (tương ứng với trạng thái St và thông tin trước đó) sẽ là:

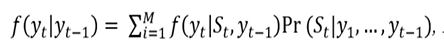
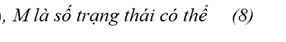
Hàm log likelihood sẽ có dạng như sau:

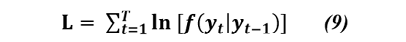
Trong đó, T là số quan sát trong tập hợp dữ liệu tác giả sử dụng phương pháp tối đa hóa giá trị kỳ vọng (Expected Maximization algorithm) được giới thiệu bởi Dempster và cộng sự (1997) để tối đa hóa giá trị ước lượng hợp lý (log likelihood) của các tham số µSt, βSt và ∑St tương ứng với St = 1,2…, M và xác suất chuyển đổi P.

Dữ liệu nghiên cứu

Dữ liệu nghiên cứu được sử dụng để ước lượng các trạng thái chuyển đổi là chỉ số VN-Index và chỉ số giá vàng theo tháng của Việt Nam trong giai đoạn 2002 - 2022, nguồn dữ liệu được thu thập tại Tổng cục Thống kê và Sở Giao dịch Chứng khoán Việt Nam (HOSE).

Hình 1 cho thấy, chỉ số VN-Index biến động theo xu hướng tăng trong giai đoạn từ tháng 01/2002 đến tháng 12/2022. Trong giai đoạn này, chỉ số VN - Index cũng có những thời điểm biến động mạnh từ tác động của các sự kiện xảy ra trên thế giới và tại Việt Nam. Cụ thể, biến động tăng mạnh trong năm 2007 và sau đó sụt giảm mạnh, do tác động từ khủng hoảng tài chính toàn cầu 2008, nhưng phục hồi và biến động nhẹ theo chiều hướng tăng lên kể từ những năm sau đó, đạt đỉnh điểm vào năm 2018 và sụt giảm mạnh kể từ cuối năm 2019 và năm 2020 do ảnh hưởng của dịch bệnh.

Tuy nhiên, thị trường cũng phục hồi và tăng mạnh vào năm 2021 khi đạt đỉnh mới vào tháng 3/2022. Trong khi đó, chỉ số giá vàng có biến động ngược chiều với chỉ số VN-Index trong giai đoạn từ tháng 01/2002 đến tháng 9/2011, nhưng biến động giảm và ổn định kể từ sau đó. Mặc dù, chỉ số giá vàng có biến động tăng và ngược chiều với chỉ số VN- Index tại một số thời điểm, nhưng mức độ biến động nhẹ hơn. Sự biến động của chỉ số giá vàng so với chỉ số VN- Index có thể được giải thích bởi sự kiểm soát và ổn định giá vàng của Ngân hàng Nhà nước nhằm kiểm soát tình trạng đầu cơ của các nhà đầu tư.