Dự báo biến động của thị trường chứng khoán các quốc gia mới nổi trong bối cảnh xung đột Nga-Ukraine
Nghiên cứu này ứng dụng và so sánh hiệu quả giữa mô hình GARCH(1,1) và E-GARCH(1,1) trong việc mô hình hóa và dự báo biến động của thị trường chứng khoán các quốc gia mới nổi trong bối cảnh xung đột Nga-Ukraine. Kết quả cho thấy, E-GARCH(1,1) là mô hình phù hợp nhất để dự báo ngắn hạn và biến động mạnh sẽ tiếp diễn trong dài hạn. Đồng thời, hiệu ứng đòn bẩy tồn tại chứng tỏ tác động từ xung đột Nga-Ukraine và các cú sốc tiêu cực trong quá khứ có xu hướng làm tăng mức độ biến động hơn so với các cú sốc tích cực. Nghiên cứu cung cấp một công cụ dự báo ngắn hạn hiệu quả cho các nhà đầu tư, giúp họ có nắm bắt được các cơ hội đầu tư phù hợp.
Đặt vấn đề
Đến thời điểm nghiên cứu, xung đột Nga-Ukraine đã kéo dài 2 năm, với nhiều diễn biến phức tạp, gây ra môi trường bất ổn lớn, đặc biệt với các quốc gia mới nổi phụ thuộc nhiều vào giao thương hàng hóa, năng lượng và dịch vụ từ Nga và Ukraine.
Báo cáo của World Bank (2023) cho rằng, xung đột này gây bất ổn thị trường năng lượng và gián đoạn kinh tế toàn cầu, nghiêm trọng hơn cả khủng hoảng xăng dầu năm 1970. Wang (2019) cho rằng, các rủi ro chính trị có thể ảnh hưởng lớn đến các thị trường tài chính mới nổi. Do đó, dự báo biến động thị trường chứng khoán (TTCK) các quốc gia mới nổi trở nên cấp thiết để xây dựng các chiến lược đầu tư và giảm thiểu rủi ro cho nhà đầu tư.
Trong lĩnh vực tài chính, mô hình GARCH đã được sử dụng rộng rãi để dự báo biến động TTCK. Mô hình này hiệu quả trong việc mô hình hóa sự biến động của chuỗi thời gian tài chính. Bên cạnh đó, mô hình E-GARCH (Exponential GARCH), được áp dụng như một phương pháp thay thế, giải quyết hạn chế của GARCH, đặc biệt trong việc mô hình hóa sự bất đối xứng của biến động. Như vậy, nghiên cứu này áp dụng cả mô hình đối xứng GARCH và bất đối xứng E-GARCH để ước tính biến động của chỉ số Thị trường mới nổi của MSCI trong bối cảnh xung đột Nga-Ukraine và so sánh hiệu quả dự báo của hai mô hình này. Qua đó, nghiên cứu này cung cấp bằng chứng thực nghiệm cho các nhà đầu tư, giúp xây dựng chiến lược đầu tư và biện pháp phòng ngừa rủi ro trong giai đoạn thị trường bất ổn.
Tổng quan nghiên cứu
Trong ba mô hình dự báo phổ biến nhất hiện nay: EWMA, ARIMA và GARCH, GARCH là mô hình chứng tỏ hiệu quả vượt trội trong dự báo biến động tài chính (Lee và cộng sự, 2017). Trong khi đó, mô hình ARIMA cũng thể hiện sự không phù hợp trong dự báo biến động bởi giả định phương sai không đổi của mô hình này và trên thực tế, biến động của lợi nhuận chỉ số TTCK thay đổi theo phương sai trong quá khứ.
Một số nghiên cứu đã khẳng định GARCH(1,1) (GARCH tiêu chuẩn) là mô hình hiệu quả nhất để dự báo biến động của TTCK. Lee và cộng sự (2017) khẳng định, GARCH(1,1) hiệu quả trong dự báo biến động TTCK Malaysia, Indonesia và Nhật Bản. Sharma và cộng sự (2021) cũng đồng quan điểm cho rằng GARCH(1,1) là mô hình tốt nhất cho TTCK của một số nền kinh tế mới nổi.
Tuy nhiên, các nghiên cứu cũng chỉ ra, TTCK không phải lúc nào cũng phản ứng đối xứng với các thông tin mới. Nelson (1991) đã giới thiệu mô hình E-GARCH, giúp mô hình hóa các hiệu ứng bất đối xứng, trong đó sự phản ứng của thị trường đối với các cú sốc âm và dương có thể khác nhau, đặc biệt trong giai đoạn biến động mạnh, khi đó các cú sốc tiêu cực có xu hướng tạo ra tác động lớn hơn. Alberg và cộng sự (2008) đã có phát hiện rằng, E-GARCH dự báo phương sai có điều kiện tốt hơn so với GARCH(1,1) và nắm bắt biến động của chỉ số S và P 500 tốt hơn. Hồ Thủy Tiên và cộng sự (2017) đã chỉ ra sự tồn tại của các hiệu ứng bất cân xứng của chỉ số VNIndex, theo đó việc ứng dụng mô hình E-GARCH(1,1) đã làm rõ ảnh hưởng rõ rệt từ các cú sốc tiêu cực bởi đại dịch COVID-19 và xung đột Nga-Ukraine tới biến động của chỉ số này.
Mặt khác, Gokan (2000) nhận thấy, GARCH(1,1) tốt hơn E-GARCH trong mô hình hóa biến động TTCK ở 7 quốc gia mới nổi. Nghiên cứu của Kosapattarapim và cộng sự (2012) khi đánh giá mô hình phù hợp nhất trong dự báo biến động TTCK các quốc gia mới nổi tại châu Á đã kết luận GARCH(1,1) là mô hình phù hợp nhất với chuỗi dữ liệu, tuy nhiên không phải lúc nào cũng đưa ra dự báo tốt nhất. Hansen và Lunde (2005) cho rằng, hiệu quả dự báo còn phụ thuộc vào loại tài sản, GARCH tuyến tính phù hợp với tiền tệ và GARCH phi tuyến tính phù hợp với cổ phiếu.
Tổng quan nghiên cứu cho thấy, mặc dù đã có nhiều nghiên cứu được thực hiện dựa trên mô hình dự báo biến động của TTCK trên thế giới, song với hiểu biết của nhóm tác giả, chưa có nghiên cứu nào thực hiện với bối cảnh các quốc gia mới nổi trong thời kỳ xung đột Nga-Ukraine. Bên cạnh đó, các kết luận về tính ưu việt của mô hình GARCH và E-GARCH trong việc dự báo biến động TTCK là không thống nhất. Do đó, nghiên cứu này ứng dụng mô hình GARCH đối xứng và bất đối xứng để dự báo biến động chỉ số TTCK các quốc gia mới nổi, so sánh hiệu quả dự báo của hai mô hình để tìm ra mô hình phù hợp nhất.
Phương pháp nghiên cứu
Dữ liệu nghiên cứu
Nghiên cứu này sử dụng dữ liệu thứ cấp là giá đóng cửa hàng ngày của chỉ số Thị trường mới nổi của MSCI (MSCI Emerging Markets Index) (EM). Chỉ số này được đưa vào nghiên cứu vì nó mang tính chất đại diện, thành phần bao gồm các doanh nghiệp có vốn hóa lớn thuộc 24 nền kinh tế mới nổi (MSCI, 2024). Dữ liệu được thu thập trong giai đoạn 2010 đến 2024, tương ứng với 3.540 quan sát từ cơ sở dữ liệu của Yahoo! Finance.
Biến động được ước tính dựa trên tỷ suất sinh lợi của chỉ số EM được xác định như sau:
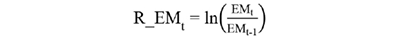
Trong đó: R_EMt là lợi suất của chỉ số EM tại thời điểm t, EMt và EMt-1 lần lượt là giá đóng cửa tại thời điểm t và t-1.
Các kiểm định và phân tích mô hình được thực hiện bằng phần mềm Eviews 12.
Phương pháp nghiên cứu
Kiểm định tính dừng và hiệu ứng ARCH
Dữ liệu nghiên cứu là chuỗi thời gian, do đó, việc kiểm tra tính dừng của dữ liệu là cần thiết và được thực hiện bằng kiểm định Augmented Dickey-Fuller (ADF). Trước khi thực hiện kiểm định hiệu ứng ARCH và xa hơn nữa là ứng dụng mô hình GARCH, chuỗi tỷ suất lợi nhuận (R_EM) phải được kiểm tra về tính không đồng nhất có điều kiện của phương sai bằng kiểm định Breusch-Pagan Lagrange (LM). Bài nghiên cứu này sử dụng thử nghiệm ARCH-LM nhằm thiết lập bằng chứng cho sự tồn tại của hiệu ứng ARCH(3).
Mô hình ARCH(q) giả định rằng phương sai có điều kiện của sai số tại thời điểm hiện tại phụ thuộc vào các sai số trong quá khứ và có phương trình như sau:
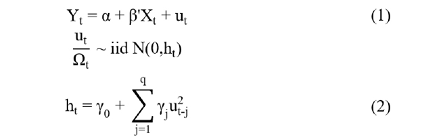
Trong đó, ht là phương sai có điều kiện tại thời điểm t.
Ước lượng mô hình GARCH và E-GARCH
Mô hình GARCH (p,q) được thể hiện qua phương trình sau :
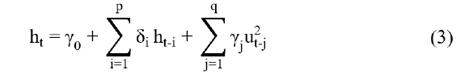
Có thể thấy, mô hình GARCH (p,q) đã kết hợp cả phần ARCH và phần GARCH để mô hình hóa phương sai có điều kiện (Bollerslev, 1986). Theo phương trình (3), thành phần 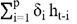 thể hiện sự phụ thuộc của phương sai hiện tại vào giá trị phương sai có điều kiện trong quá khứ. Bên cạnh đó, thành phần
thể hiện sự phụ thuộc của phương sai hiện tại vào giá trị phương sai có điều kiện trong quá khứ. Bên cạnh đó, thành phần 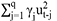 chỉ ra sự ảnh hưởng của các giá trị sai số trong quá khứ lên tới phương sai hiện tại.
chỉ ra sự ảnh hưởng của các giá trị sai số trong quá khứ lên tới phương sai hiện tại.
Tuy nhiên, ARCH(q) và GARCH (p,q) tồn tại nhược điểm là đều dựa trên bình phương của phương sai để mô hình hóa phương sai có điều kiện. Vì bình phương của một số luôn không âm nên mô hình sẽ phản ứng như nhau với các giá trị ut dương và âm có cùng độ lớn, dẫn đến tính đối xứng trong cách các mô hình này phản ứng với các cú sốc trong chuỗi thời gian.
Để khắc phục nhược điểm này, Nelson (1991) đã phát triển mô hình E-GARCH nhằm giải quyết được vấn đề nêu trên mà không cần phải đặt điều kiện là phương sai là số dương và giúp dễ dàng phản ánh hiệu ứng đòn bẩy.
Mô hình E-GARCH có dạng:
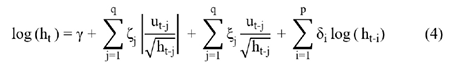 Thông qua tham số ξj, mô hình cho phép các cú sốc tiêu cực âm có tác động khác với các cú sốc tiêu cực dương cùng kích thước. Nếu ξj khác 0, điều này sẽ tạo ra sự bất đối xứng. Thêm vào đó, hiệu ứng đòn bẩy sẽ được phản ánh khi các cú sốc tiêu cực làm tăng phương sai có điều kiện nhiều hơn so với các cú sốc tích cực có cùng kích thước.
Thông qua tham số ξj, mô hình cho phép các cú sốc tiêu cực âm có tác động khác với các cú sốc tiêu cực dương cùng kích thước. Nếu ξj khác 0, điều này sẽ tạo ra sự bất đối xứng. Thêm vào đó, hiệu ứng đòn bẩy sẽ được phản ánh khi các cú sốc tiêu cực làm tăng phương sai có điều kiện nhiều hơn so với các cú sốc tích cực có cùng kích thước.
Dự báo biến động của chỉ số EM và so sánh hiệu quả mô hình
Tiếp theo, mô hình GARCH và E-GARCH được sử dụng để dự báo và so sánh hiệu quả.
Để lựa chọn mô hình phù hợp nhất với dữ liệu nghiên cứu, nhóm tác giả dựa vào các tiêu chí giá trị nhỏ nhất đối với tiêu chuẩn thông tin (AIC) và giá trị lớn nhất đối với Log-likelihood. Tiêu chí Log-likelihood đánh giá mức độ khớp hệ số giữa các mô hình, trong khi tiêu chí AIC sử dụng giá trị tuyệt đối lớn hơn để chỉ ra mức độ khớp dữ liệu tốt hơn.
Nghiên cứu thực hiện dự báo tĩnh (static forecast) và so sánh hiệu suất của hai mô hình GARCH trên thông qua các tiêu chí sau: lỗi bình phương trung bình (MAE), lỗi bình phương trung bình căn bậc hai (RMSE) và lỗi phần trăm tuyệt đối trung bình (MAPE).
Kết quả và thảo luận
|
Bảng 1: Thống kê mô tả và kiểm định tính dừng của tỷ suất lợi nhuận |
||
|
R_EM |
||
|
Mean |
0,000 |
|
|
Median |
0,000 |
|
|
Max |
0,083 |
|
|
Min |
-0,109 |
|
|
Std. Dev. |
0,011 |
|
|
Skewness |
-0,515 |
|
|
Kurtosis |
10,196 |
|
|
Jarque-Bera |
7795,297*** |
|
|
Observations |
3540 |
|
|
ADF test statistic |
-25,868*** |
|
Nguồn: Kết quả phân tích số liệu của nhóm tác giả |
||
|
Bảng 2: Kết quả kiểm định hiệu ứng ARCH |
|
|
R_EM |
|
|
F-Stat |
356,4462 |
|
Obs*R-squared |
821,7568 |
|
Prob.F |
0,0000 |
|
Prob.Chi-Square (3) |
0,0000 |
|
Nguồn: Kết quả phân tích số liệu của nhóm tác giả |
|
|
Bảng 3: Kết quả ước tính của mô hình GARCH(1,1) và E-GARCH(1,1) |
||
|
Các hệ số |
GARCH(1,1) |
E-GARCH(1,1) |
|
Phương trình trung bình (Coefficient equation) |
||
|
µ (hằng số) |
0,000*** [2,589] |
0,000 [0,890] |
|
λ (phần bù rủi ro) |
-0,148*** [-8,636] |
-0,150*** [-9,043] |
|
Phương trình phương sai (Variance equation) |
||
|
ω (hằng số C) |
3,50E-06*** [5,590] |
-0,383*** [8,467] |
|
α (hiệu ứng ARCH) |
0,079*** [13,092] |
0,134*** [11,174] |
|
γ (hiệu ứng bất đối xứng) |
N/A |
-0,073*** [-10,603] |
|
β (hiệu ứng GARCH) |
0,892*** [101.002] |
0,970*** [210,370] |
|
α + β |
0,971 |
1,103 |
|
Các tiêu chí đánh giá |
||
|
Log likelihood (LL) |
11164,59 |
11188,76 |
|
Akaike info criterion (AIC) |
-6,307 |
-6,320 |
|
Ghi chú: Thống kê z trong các ngoặc vuông; *** p-value < 0,01 |
||
|
Nguồn: Kết quả phân tích số liệu của nhóm tác giả |
||
|
Bảng 4: Kết quả sai số dự báo của mô hình GARCH(1,1) và E-GARCH(1,1) |
|||
|
MAE |
RMSE |
MAPE |
|
|
GARCH(1,1) |
0,004839 |
0,006495 |
119,316 |
|
E-GARCH(1,1) |
0,004814 |
0,006551 |
109,435 |
|
Nguồn: Kết quả phân tích số liệu của nhóm tác giả |
|||
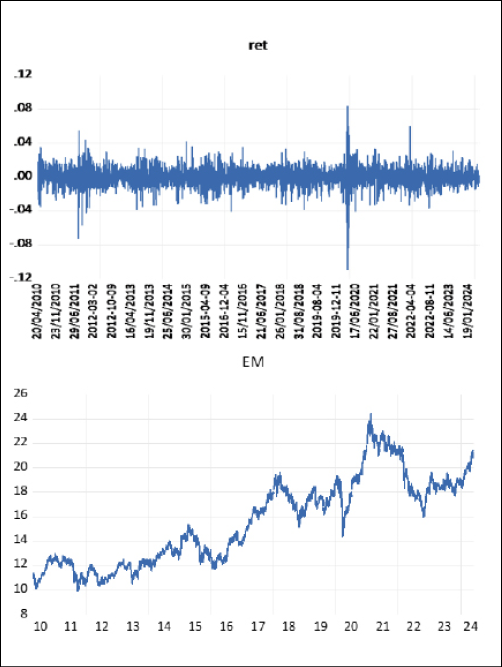
Bảng 1 cho thấy, khoảng dao động của dữ liệu là khá rộng (từ -0,109 đến 0,083). Chỉ số EM có độ lệch (skewness) âm (-0,515) trong lợi nhuận, chứng tỏ chỉ số này có lợi nhuận thấp. Ngoài ra, hệ số nhọn (kurtosis) cao (10,196) phản ánh phân phối leptokurtic, ngụ ý rằng lợi suất không đối xứng, xuất hiện lợi suất được ghi nhận rất cao/thấp trong giai đoạn năm 2010 đến 2024. Bên cạnh đó, lợi nhuận không phân phối chuẩn, do kết quả kiểm định phân phối chuẩn (Jarque-Bera) ở mức rất cao và p-value có mức ý nghĩa thống kê 1%, giúp bác bỏ giả thuyết chuỗi dữ liệu tuân theo phân phối chuẩn.
Kết quả nghiên cứu cho thấy, R_EM dao động với biên độ lớn xung quanh giá trị trung bình không đổi của chuỗi dữ liệu và có phương sai thay đổi theo thời gian. Bên cạnh biến động rất mạnh dễ dàng nhận thấy, trong giai đoạn COVID-19, chuỗi tỷ suất lợi nhuận còn chứng kiến một cụm biến động mạnh và giá đóng cửa giảm mạnh vào khoảng thời gian quý II/2022 - thời điểm đánh dấu sự căng thẳng leo thang của xung đột Nga-Ukraine.
Tiếp theo, để đánh giá tính dừng của chuỗi, kiểm định nghiệm đơn vị theo phương pháp ADF. Bảng 1 cho thấy, giá trị tuyệt đối của giá trị thống kê kiểm định là 25,868 và có mức ý nghĩa thống kê 1%; nên ta bác bỏ giả thuyết H0. Do đó, có thể kết luận rằng chuỗi dữ liệu nghiên cứu có tính dừng.
Theo Engle (1982), trước khi thực hiện mô hình kiểm định GARCH, trước tiên phải kiểm tra hiệu ứng ARCH để xác định xem mô hình ARCH(q) có phù hợp với chuỗi dữ liệu đã cho hay không. Nhằm đơn giản hóa, mô hình chỉ chứa hằng số làm biến hồi quy và cho phép phương sai ht dựa vào 3 độ trễ (lag-length) của các giá trị phương sai trong quá khứ.
Theo Bảng 2, giá trị xác suất của cả thống kê F và thống kê LM đều bằng 0, đáp ứng tiêu chí là nhỏ hơn giá trị tới hạn ở mức ý nghĩa 1%. Nói cách khác, kiểm định hiệu ứng ARCH(3) đã cung cấp bằng chứng mạnh mẽ để bác bỏ H0. Điều này cho thấy, có tồn tại hiệu ứng ARCH trong chuỗi thời gian R_EM.
Từ đó, mô hình GARCH(1,1) và E-GARCH(1,1) có kết quả ước lượng như Bảng 3.
Đối với mô hình GARCH(1,1), cả 2 tham số ARCH và GARCH (α và β) đều có ý nghĩa thống kê ở mức 1%. Điều này chứng minh, mô hình GARCH(1,1) là phù hợp để miêu tả sự biến động của chuỗi dữ liệu. Ngoài ra, tổng α + β = 0,971 gần bằng 1 nhưng nhỏ hơn 1 chỉ ra rằng mô hình có tính bền vững cao, có khả năng nắm bắt được các đặc điểm chính của sự biến động trong chuỗi tỷ suất lợi nhuận và khẳng định lại xu hướng ảnh hưởng lâu dài của các cú sốc đến biến động của lợi suất chỉ số TTCK. Hay nói cách khác, mức độ biến động cao hiện tại có thể dự báo mức độ biến động cao trong tương lai.
Đối với mô hình E-GARCH(1,1), tham số γ (= -0,073) nhỏ hơn 0 và có ý nghĩa thống kê ở mức 1%. Giá trị âm của γ đã chứng minh sự tồn tại của hiệu ứng đòn bẩy (bất đối xứng) trên chuỗi thời gian EM; đồng thời, thể hiện rằng các cú sốc tiêu cực có xu hướng làm tăng sự biến động hơn các cú sốc tích cực, cụ thể là các cú sốc khiến chỉ số TTCK tăng/giảm đột ngột tại thời điểm t sẽ làm giảm/tăng 7,3% mức thay đổi của chỉ số TTCK tại thời điểm t+1. Ngoài ra, tổng của 2 tham số α và β lớn hơn 1 (1,103). Khi đó, phương sai có điều kiện có xu hướng tăng dần theo thời gian. Điều này có nghĩa là sự biến động của chuỗi dữ liệu sẽ không quay trở lại mức trung bình dài hạn mà sẽ tiếp tục tăng lên; dẫn đến tính bất ổn cao của mô hình, khiến kết quả dự báo thiếu tin cậy.
Căn cứ theo các tiêu chí đánh giá mô hình phù hợp với dữ liệu, ta thấy mô hình E-GARCH(1,1) thỏa mãn toàn bộ điều kiện của các tiêu chí trên. Như vậy, mặc dù tính bền vững không bằng mô hình GARCH(1,1) nhưng vẫn ưu việt hơn trong việc mô hình hóa các tính chất phi tuyến tính, đặc biệt khi dữ liệu nghiên cứu được chứng minh là có tồn tại hiệu ứng bất đối xứng.
Tiếp theo, khả năng dự đoán của các mô hình được đánh giá dựa trên ba phép đo: MAE, RMSE và MAPE. Kết quả của các chỉ số này càng thấp thì mô hình dự báo sự biến động của chuỗi tỷ suất lợi nhuận càng sát với các giá trị thực tế. Mức độ biến động trong tháng cuối của tập dữ liệu thử nghiệm (từ ngày 01/5/2024 đến ngày 29/5/2024) được ước tính thông qua mô hình dự báo có kết quả như Bảng 4.
Dựa vào 2/3 tiêu chí (MAE và MAPE), có thể thấy E-GARCH(1,1) là mô hình hợp lý hơn khi áp dụng vào việc dự báo biến động chỉ số TTCK mới nổi trong giai đoạn mẫu kiểm định trên. Tuy nhiên, vì phương sai có điều kiện của mô hình E-GARCH(1,1) tăng dần theo thời gian nên mô hình không thích hợp để dự báo dài hạn. Do vậy, nhóm tác giả kết luận rằng E-GARCH(1,1) là mô hình phù hợp nhất với dữ liệu nghiên cứu và cũng là mô hình dự báo ngắn hạn hiệu quả hơn so với GARCH(1,1) khi dự báo biến động của R_EM.
Kết luận
Kết quả phân tích cho thấy, trong dữ liệu nghiên cứu xuất hiện hiệu ứng đòn bẩy, đồng thời, các biến động trong quá khứ có ảnh hưởng lớn tới biến động trong tương lai. Do vậy, với diễn biến căng thẳng leo thang của cuộc xung đột, TTCK các quốc gia mới nổi được dự báo sẽ xuất hiện những biến động lớn trong lợi suất hàng ngày, vì thế tăng tính hấp dẫn đối với các nhà đầu tư vào thị trường này.
Nghiên cứu này đưa ra kết luận E-GARCH(1,1) là mô hình dự báo ngắn hạn hiệu quả nhất đối với biến động TTCK các quốc gia mới nổi. Từ đó, giúp các nhà đầu tư nắm bắt được các cơ hội đầu tư phù hợp. Kết quả này đồng thuận với các nghiên cứu trước đây của Hansel và Lunde (2005), Albert và cộng sự (2008) và trái ngược với kết luận đưa ra bởi Gokan (2000). Tuy nhiên, nghiên cứu này chỉ giới hạn ở phân tích đơn biến và do đó, đã hạn chế phạm vi nghiên cứu về các cơ hội đa dạng hóa đầu tư. Như vậy, hướng nghiên cứu là áp dụng mô hình GARCH đa biến để phân tích cơ hội đa dạng hóa giữa các quốc gia mới nổi.
Tài liệu tham khảo:
- Hồ Thủy Tiên, Hồ Thu Hoài và Lê Văn Toàn (2017), Mô hình hóa biến động thị trường chứng khoán: Thực nghiệm từ Việt Nam, Tạp chí Khoa học ĐHQGHN: Kinh tế và Kinh doanh, 3(33), 21–31;
- Alberg, D., Shalit, H. và Yosef, R. (2008), Estimating stock market volatility using asymmetric GARCH models, Applied Financial Economics, 18(15), 1201–1208;
- Bollerslev, T. (1986), A conditionally heteroskedastic time series model for speculative prices and rates of return, The Review of Economics and Statistics, 542–547;
- Engle, R. F. (1982), Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation, Econometrica, 50(4), 987;
- Gokcan, S. (2000), Forecasting volatility of emerging stock markets: linear versus non-linear GARCH models, Journal of Forecasting, 19(6), 499–504;
- Hansen, P. R. và Lunde, A. (2005), A forecast comparison of volatility models: does anything beat a GARCH(1,1)? Journal of Applied Econometrics, 20(7), 873–889;
- Kosapattarapim, C., Lin, Y.X., và McCrae, M. (2012), Evaluating the volatility forecasting performance of best fitting GARCH models in emerging Asian stock markets. International Journal of Mathematics và Statistics, 12(2), 1–15;
- Lee, N. S. K., Nguyen, N. L. T. P. và Sy, M. O. (2017), Comparative Study of Volatility Forecasting Models: The Case of Malaysia, Indonesia, Hong Kong and Japan Stock Markets, Economics World, 5(4), 299-310.



















