Từ đó ứng dụng vào mô hình hóa bộ dữ liệu về chỉ số VN-Index, chỉ số chứng khoán của Sở Giao dịch Chứng khoán TP. Hồ Chí Minh (HSX) nhằm phản ánh diễn biến giá cả chung của toàn bộ cổ phiếu đang niêm yết trên HSX, phụ thuộc vào các yếu tố có ảnh hưởng như chỉ số chứng khoán Mỹ, tỷ giá, giá dầu, giá vàng. Thông qua các mô hình hồi quy với số lượng quan sát khác nhau, nhóm nghiên cứu đưa ra các nhận định và đánh giá tính ổn định của các mô hình hồi quy.

Giới thiệu

Mô hình hồi quy cổ điển (OLS) thường được sử dụng trong xem xét sự ảnh hưởng của các biến độc lập (biến giải thích) với biến phụ thuộc (biến được giải thích), từ đó xem xét tính phù hợp cũng như dự báo. Mặc dù, đây không phải là mô hình mới, nhưng tính hữu dụng và dễ tiếp cận của mô hình nên thường được ứng dụng khá phổ biến trong nhiều lĩnh vực (Long, J. S., & Ervin, L. H., 2000) và giúp lựa chọn các mô hình hồi quy phù hợp nhất (Shi, P., & Tsai, C. L., 2002; Norris, C. M., Ghali, W. A., Saunders, L. D., Brant, R., Galbraith, D., Faris, P., ... & APPROACH Investigators, 2006; Ferrari, S., & Cribari-Neto, F., 2004; Rejeb, A. B., & Arfaoui, M., 2016).

Đối với giá chứng khoán cũng không ngoại lệ, khi mô hình hồi quy OLS được các nhà nghiên cứu sử dụng ngày càng nhiều. Các mô hình hồi quy có rất nhiều ứng dụng trong mô hình hóa suất sinh lợi giá chứng khoán thông qua mô hình hồi quy chịu ảnh hưởng của các yếu tố như: Chỉ số S&P500, chỉ số sản xuất công nghiệp, tỷ lệ thất nghiệp, giá trị phi nông nghiệp, chỉ số tâm lý tiêu dùng, chỉ số giá tiêu dùng (Grima, S., & Caruana, L., 2017, October) theo mô hình hồi quy OLS. Ngoài ra, còn được dùng cho mô hình hồi quy suất sinh lợi giá chứng khoán dựa vào giá dầu OPEC, chỉ số S&P500 của các nước vùng vịnh GCC (Bahrain, Kingdom of Saudi Arabia, Kuwait, Qatar, Sultanate of Oman, and United Arab Emirates (UAE)) (Nusair, S. A., & Al-Khasawneh, J. A., 2018).

Bên cạnh đó, sự mở rộng của mô hình hồi quy OLS thành mô hình hồi quy phân vị (từ mô hình OLS cổ điển) cũng mang lại nhiều lợi ích. Đối với mô hình hồi quy phân vị, các nhà nghiên cứu có thể đưa ra được một số kết luận về tác động tùy vào từng mức phân vị của các yếu tố ảnh hưởng đối với giá chứng khoán. So với mô hình hồi quy cổ điển với các ước lượng của mô hình hồi quy biểu diễn thông qua giá trị trung bình, thì mô hình hồi quy phân vị biểu diễn thông qua giá trị trung vị và các mức phân vị mong muốn nên tạo ra được một bức tranh tổng thể. Thêm vào đó, mô hình suất sinh lợi giá chứng khoán còn được biểu diễn thông qua biến định tính, chẳng hạn như độ bất ổn chính trị thông qua mô hình hồi quy phân vị (Guo, P., Zhu, H., & You, W., 2018). Do đó, so với mô hình hồi quy cổ điển với các ước lượng của mô hình hồi quy biểu diễn thông qua giá trị trung bình, thì mô hình hồi quy phân vị biểu diễn thông qua giá trị trung vị và các mức phân vị mong muốn nên tạo ra được một bức tranh tổng thể.

Mặc dù, trong các nghiên cứu dù có dựa vào mô hình hồi quy cổ điển OLS, mô hình hồi quy phân vị đều dựa vào dữ liệu lịch sử của các biến đó. Tuy nhiên, chưa có nghiên cứu nào phân tích các mô hình hồi quy dựa vào dữ liệu lịch sử bao nhiêu là đủ. Thông thường, các nghiên cứu sẽ có được một bộ dữ liệu lịch sử, chạy ra mô hình và các kết luận dựa vào mô hình đó. Thực tiễn nghiên cứu cho thấy, một vấn đề rất lớn đặt ra là khi dữ liệu lịch sử là chuỗi thời gian, mô hình cần lấy dữ liệu quá khứ bao nhiêu là phù hợp nhất. Ngoài ra, một vấn đề đáng lưu tâm khác là các hệ số của mô hình hồi quy có ổn định khi thêm bớt số lượng các quan sát hay không. Nếu mô hình có ít sự thay đổi của các hệ số, mới đảm bảo được rằng mô hình đó có tính ổn định, từ đây có thể dựa vào mô hình hồi quy trong việc ước lượng các giá trị của biến phụ thuộc cũng như dự báo.

Cần lưu ý rằng, các nghiên cứu về mô hình hóa giá chứng khoán được nghiên cứu khá phổ biến trên thế giới, tuy nhiên, đối với thị trường chứng khoán Việt Nam có các đặc trưng riêng, hơn nữa, với dữ liệu cập nhật đến thời điểm hiện tại, khi bắt đầu chịu các ảnh hưởng từ dịch bệnh cần có các nghiên cứu chuyên sâu hơn. Dựa trên những phân tích đó, nhóm nghiên cứu xem xét số lượng dữ liệu lịch sử phù hợp trong ước lượng mô hình, đồng thời nghiên cứu sự biến đổi các tham số ước lượng của mô hình hồi quy với nội dung tập trung vào “Tính ổn định của mô hình hồi quy trong mô hình hóa giá chứng khoán Việt Nam”.

Mô hình hồi quy

Hơn nữa, các dữ liệu trong nghiên cứu này dựa vào dữ liệu chuỗi thời gian, song các kiểm định tính dừng của dữ liệu thông qua các chỉ số ACF,PACF, nghiệm đơn vị thông qua Dickey–Fuller hoặc Phillips–Perron.

Tuy nhiên, các kiểm định trên thực tế là kiểm tra tính phân phối chuẩn của dữ liệu. Vì các chỉ số trong mô hình phân tích dao động lên xuống và đa số tập trung trong một khoảng giá trị, do đó, đảm bảo dữ liệu nghiên cứu là dừng.

Bởi vậy, các giá trị chuỗi thời gian sẽ chịu ảnh hưởng của các giá trị trong quá khứ. Do đó, nhóm nghiên cứu xây dựng mô hình hồi quy với các dữ liệu lịch sử, cụ thể, mô hình hồi quy được xây dựng dựa vào bộ dữ liệu lịch sử bao gồm n thời điểm lịch sử (quan sát) {z_t,z_t-1,...,z_t-n+1}, với số lượng n lần lượt là 50, 100, 150, 250, 500, 1000 dữ liệu lịch sử.

Tức là, mỗi khi cập nhật thêm một dữ liệu mới thì bỏ bớt một dữ liệu xa thời điểm nghiên cứu nhất. Khi đó, nhóm nghiên cứu sẽ đánh giá sự ổn định của các mô hình hồi quy với mỗi bộ dữ liệu lịch sử về sự thay đổi của các độ phù hợp mô hình hồi quy, các hệ số ứng với các biến độc lập. Từ đây, đánh giá độ phù hợp đúng trung bình cao nhất nhằm đưa ra các nhận xét về dữ liệu lịch sử phù hợp nhất đối với mỗi bộ dữ liệu nhằm đảm bảo tính ổn định và độ phù hợp trung bình cao nhất.

Ứng dụng vào bộ dữ liệu giá chứng khoán Việt Nam

Giới thiệu bộ dữ liệu

Bộ dữ liệu nghiên cứu của Thomson Reuters lấy tại Trung tâm Nghiên cứu Kinh tế - Tài chính (Đại học Kinh tế - Luật, Đại học Quốc gia TP. Hồ Chí Minh) bao gồm: Chỉ số VN-Index, Chỉ số trung bình công nghiệp Dow Jones, tỷ giá EUR/VND của Ngân hàng Nhà nước Việt Nam (đơn vị: nghìn đồng), tỷ giá USD/VND theo Ngân hàng Nhà nước Việt Nam (đơn vị nghìn đồng), Chỉ số S&P500 (Standard & Poor), giá vàng tại Mỹ (đơn vị USD/ounce), giá dầu thô WTI là giá dầu ở giếng khoan Mỹ theo ngày (đơn vị tính USD/thùng).

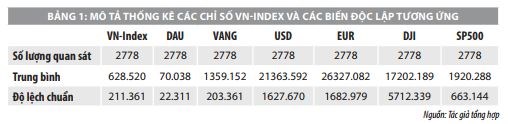
Các chỉ số thống kê mô tả của các chỉ số

Bảng mô tả thống kê các chỉ số VN-Index (biến phụ thuộc) và các biến độc lập tương ứng, trong khoảng thời gian từ ngày 02/01/2009 đến ngày 03/06/2020:

Mô hình hồi quy của tất cả các giá trị

Để kiểm tra tính đúng đắn của mô hình nghiên cứu, nghiên cứu này chạy mô hình hồi quy OLS của tất cả các giá trị. Kết quả về độ phù hợp R^2=92.7% chứng tỏ mô hình nghiên cứu phù hợp. Cụ thể, mô hình hồi quy OLS có dạng sau:

VN-Index=589.2356 + 0.0886×DJI + 0.0153× EUR -0.0428× USD -0.388× SP500 -0.0971× VANG -1.3795× DAU+e

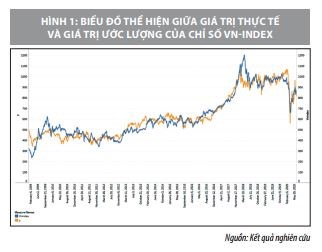
Minh họa kết quả giữa giá trị thực tế và giá trị ước lượng được dựa vào mô hình hồi quy được biểu diễn theo Hình 1. Kết quả cho thấy, có sự tương đồng giữa giá trị thực tế VN-Index màu xanh dương và giá trị ước lượng được theo mô hình y màu cam.      

Mô hình hồi quy trượt

Trong đó µβ_i là trung bình và Seβ_i là độ lệch chuẩn của các giá trị {β_0i,β_1i,...,β_hi,...}.

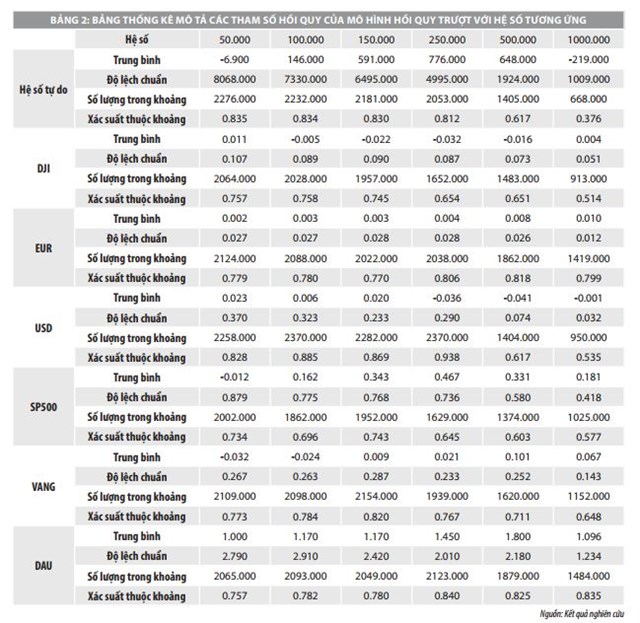
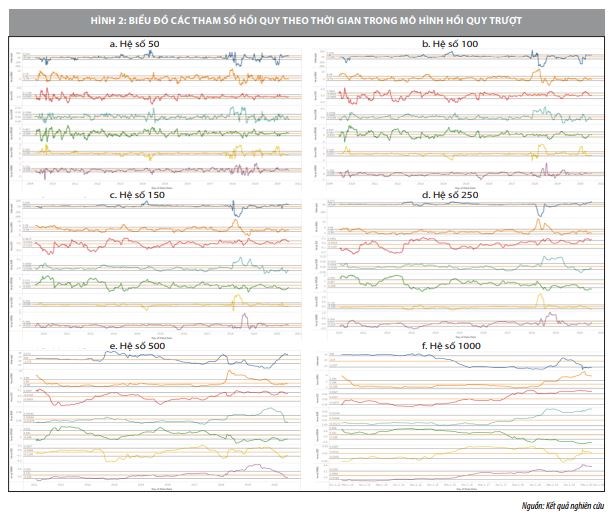
Minh họa các công thức trên, nhóm nghiên cứu sử dụng mô hình hồi quy trượt với các bộ giá trị tương ứng (hệ số) n là 50, 100, 150, 250, 500, 1000. Bộ các tham số ước lượng của các mô hình hồi quy trượt với hệ số chạy được biểu diễn trong Hình 2:

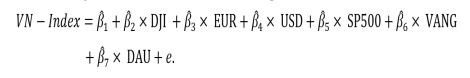
Hình 2 thể hiện biểu đồ các tham số hồi quy theo thời gian trong mô hình hồi quy trượt, trong đó 3 đường thẳng song song với trục hoành của mỗi tham số  thể hiện các chỉ số trung bình của các tham số , cận trên là +Se() và cận dưới µ()-Se().

Thông qua Hình 2, nhóm nghiên cứu nhận thận thấy các tham số của mô hình hồi quy không ổn định khi dựa vào giá trị lịch sử càng nhiều, tương ứng n càng lớn. Trong trường hợp, mô hình hồi quy trượt với n= 50 và 100 thể hiện sự ổn định nhất của các tham số hồi quy, tương ứng mô hình hồi quy ổn định nhất. Cụ thể, các kết quả số về các giá trị trung bình, độ lệch chuẩn, tỷ lệ các tham số hồi quy thuộc khoảng cận trên là µ()+Se() và cận dưới µ()-Se() được biểu diễn thông qua Bảng 2.

Kết luận

Mô hình hồi quy tuyến tính là một công cụ đơn giản với các ứng dụng trong nhiều lĩnh vực không chỉ trong lĩnh vực thống kê mà ứng dụng trong tất cả các lĩnh vực cần quan tâm đến ước lượng và dự báo, đặc biệt đối với các nghiên cứu trong lĩnh vực chứng khoán. Do đó, vấn đề cần quan tâm về tính phù hợp của mô hình hồi quy, sao cho đảm bảo mô hình hồi quy có thể sử dụng chính xác cho các suy luận tiếp theo.

Đặc biệt, khi mô hình hồi quy áp dụng đối với dữ liệu chuỗi thời gian, chúng ta không chỉ sử dụng mô hình hồi quy dựa trên tất cả các giá trị dữ liệu lịch sử có thể có. Điều này dẫn tới, những dữ liệu lịch sử quá xa thì không phản ánh đúng tình trạng hiện tại. Hơn thế nữa, mỗi khi dữ liệu được cập nhật, các tham số của mô hình hồi quy trượt sẽ thay đổi. Vì vậy, cần phải đảm bảo tính không sai khác nhiều của các tham số ước lượng trong mô hình hồi quy, hay chính là tính ổn định của mô hình hồi quy cần phải được nghiên cứu một cách chi tiết.

Trong bài viết này, nhóm nghiên cứu xây dựng mô hình hồi quy trượt xem xét chỉ số VN-Index phụ thuộc vào các chỉ số, bao gồm: Chỉ số trung bình công nghiệp Dow Jones, tỷ giá EUR/VND, tỷ giá USD/VND, chỉ số S&P500, giá vàng và giá dầu thô. Kết quả của mô hình hồi quy trượt thể hiện kết quả ổn định tốt hơn với các dữ liệu lịch sử là dựa vào 50 và 100 ngày dữ liệu lịch sử. Điều này thể hiện tính hợp lý cho các nghiên cứu về dự báo dựa vào dữ liệu lịch sử gần nhất vừa đảm bảo cung cấp thông tin cập nhật nhất, vừa đảm bảo tính ổn định nhất.

Phân tích thực tiễn của thị trường chứng khoán Việt Nam và từ kết quả nghiên cứu này cho thấy, chỉ số VN-Index chịu sự tác động mạnh của thị trường chứng khoán Mỹ thông qua chỉ số trung bình công nghiệp Dow Jones và chỉ số S&P500. Bên cạnh đó, thị trường chứng khoán Việt Nam chịu sự tác động của các tỷ giá phản ánh sức mạnh của các nền kinh tế thông qua các tỷ giá EUR/VND và tỷ giá USD/VND. Ngoài ra, thị trường chứng khoán Việt Nam cũng chịu sự tác động của tình hình sản xuất và biến động chính trị của thế giới thông qua giá vàng và giá dầu thô. Đây là các tín hiệu cho các nhà nghiên cứu và đầu tư trong nghiên cứu các điểm đặc trưng của thị trường chứng khoán Việt Nam.

Thực tế cho thấy, hồi quy phân vị dựa vào các điểm phân vị của hàm phân phối xác suất của các biến phụ thuộc, tức là chỉ ra dạng phân phối xác suất của biến phụ thuộc tại các mức phân vị. Do đó, nếu có thể tốt hơn thì nghiên cứu dựa vào mô hình hồi Bayes (Bolstad, W. M., & Curran, J. M., 2016; Gelman, A., Carlin, J. B., Stern, H. S., Dunson, D. B., Vehtari, A., & Rubin, D. B., 2013) sẽ xác định được đầy đủ dạng phân phối xác suất của các biến cũng như các tham số, thay vì các điểm thưa trong hồi quy phân vị. Do đó, trong thời gian tới, nhóm tác giả sẽ mở rộng về mô hình hồi quy Bayes và và xét tính ổn định của mô hình hồi quy Bayes tương ứng. Đồng thời, kết quả nghiên cứu này cũng mở ra thêm các hướng nghiên cứu mới cho các nhà nghiên cứu về tính ổn định của mô hình hồi quy trong mô hình hóa giá chứng khoán Việt Nam.

Tài liệu tham khảo:

1. Bolstad, W. M., & Curran, J. M. (2016), Introduction to Bayesian statistics. John Wiley & Sons;

2. Ferrari, S., & Cribari-Neto, F. (2004), Beta regression for modelling rates and proportions. Journal of applied statistics, 31(7), 799-815;

3. Gelman, A., Carlin, J. B., Stern, H. S., Dunson, D. B., Vehtari, A., & Rubin, D. B. (2013), Bayesian data analysis. CRC press;

4. Guo, P., Zhu, H., & You, W. (2018), Asymmetric dependence between economic policy uncertainty and stock market returns in G7 and BRIC: A quantile regression approach. Finance Research Letters, 25, 251-258;

5. Kutner, M. H., Nachtsheim, C. J., Neter, J., & Li, W. (2005), Applied linear statistical models (Vol. 5). New York: McGraw-Hill Irwin;

6. Long, J. S., & Ervin, L. H. (2000), Using heteroscedasticity consistent standard errors in the linear regression model. The American Statistician, 54(3), 217-224;

7. Norris, C. M., Ghali, W. A., Saunders, L. D., Brant, R., Galbraith, D., Faris, P., ...& APPROACH Investigators. (2006), Ordinal regression model and the linear regression model were superior to the logistic regression models. Journal of clinical epidemiology, 59(5), 448-456;

8. Nusair, S. A., & Al-Khasawneh, J. A. (2018), Oil price shocks and stock market returns of the GCC countries: empirical evidence from quantile regression analysis. Economic Change and Restructuring, 51(4), 339-372;

9. Rejeb, A. B., & Arfaoui, M. (2016), Financial market interdependencies: A quantile regression analysis of volatility spillover. Research in International Business and Finance, 36, 140-157;

10. Shi, P., & Tsai, C. L. (2002), Regression model selection - A residual likelihood approach, Journal of the Royal Statistical Society: Series B (Statistical Methodology), 64(2), 237-252.