Thông qua kết quả nghiên cứu này, khi áp dụng vào tình hình thực tiễn của Việt Nam, có thể giúp dự báo GDP trong giai đoạn tới thông qua sự tăng/giảm các dữ liệu lịch sử đồng thời có tính đến các đặc điểm riêng của nền kinh tế Việt Nam trong bối cảnh Cách mạng công nghiệp 4.0.

Đặt vấn đề

Phân tích mô hình với dữ liệu bảng đang trở thành xu hướng chung mà các nhà nghiên cứu thường sử dụng trong thời gian gần đây, đặc biệt ứng dụng đối với các chỉ số kinh tế vĩ mô (Cermeño, R., & Grier, K. B., 2006) dạng dữ liệu bảng. Trong khi đó, đối với các mô hình áp dụng dữ liệu chuỗi thời gian, để xây dựng mô hình phù hợp nhất với dữ liệu và kiểm soát sai số tối ưu nhất, mô hình GARCH và các dạng hiệu chỉnh của mô hình GARCH luôn là sự lựa chọn hàng đầu của giới nghiên cứu.

Thông qua dữ liệu bảng, dữ liệu có thể được mô tả một cách đa dạng các thông tin về các cá nhân, các doanh nghiệp, các địa phương, các quốc gia… theo các mốc thời gian nên có các so sánh tương quan hơn so với việc chỉ xem xét các chỉ số riêng lẻ theo chuỗi thời gian hoặc chỉ xem xét tại một thời điểm theo dữ liệu chéo. Tất nhiên, để phù hợp với thực tiễn, việc nghiên cứu các mô hình với dữ liệu bảng cũng cần có các điều chỉnh phù hợp (Baltagi, 2006) như kiểm định nghiệm đơn vị với dữ liệu bảng (Pesaran, 2007), kiểm định tính phương sai sai số thay đổi động trong trường hợp dữ liệu bảng (Pesaran, M. H., Shin, Y., & Smith, R. P., 1999)…

Thông qua việc ứng dụng bộ dữ liệu GARCH bảng đối với bộ dữ liệu kinh tế vĩ mô của sáu quốc gia châu Mỹ Latinh từ năm 2005 đến năm 2015 do World Bank cung cấp, nghiên cứu này xây dựng một quy trình ước lượng và lựa chọn mô hình GARCH với dữ liệu bảng phù hợp nhất với bộ dữ liệu. Các kết quả được thực hiện với bộ dữ liệu chỉ số kinh tế vĩ mô với các mô hình tối ưu khắc phục được các hết các vi phạm giả thuyết của mô hình hồi quy. Đồng thời, việc áp dụng mô hình GARCH với dữ liệu bảng khi phân tích đa ngành, đa lĩnh vực các vấn đề kinh tế - xã hội cũng sẽ chính xác, hiệu quả hơn, góp phần vào việc dự báo xu hướng GDP của một quốc gia thông qua sự thay đổi của các dữ liệu lịch sử.

Mô hình GARCH và mô hình GARCH bảng trong nghiên cứu

Trong các mô hình nghiên cứu về chuỗi thời gian như ARMA hay ARIMA, các phương sai của sai số thường được giả định là các hằng số. Tuy nhiên, trong thực tiễn, đặc biệt là đối với các chuỗi chứng khoán và tài chính, luôn tồn tại những cú sốc kinh tế thường đến bất ngờ dẫn đến phương sai của sai số không còn là hằng số. Sự biến đổi này là một nhân tố mà mô hình ARMA hay ARIMA theo cách thông thường không thể giải thích được, dẫn đến mô hình sẽ có kết quả không chính xác. Mô hình mô tả được hiện tương phương sai sai số thay đổi này chính là mô hình ARCH, trong đó phương sai sai số tại thời điểm bất kỳ sẽ phụ thuộc vào các bình phương có trọng số của các sai số ở những giai đoạn trước đó. Các ứng dụng của mô hình ARCH trong kinh tế và tài chính được áp dụng hiệu quả đối với những chuỗi tăng dần (hoặc giảm dần) theo chu kì như giá chứng khoán, GDP, quy mô dân số… Bên cạnh đó, khi xem xét các phương sai sai số như trong mô hình ARCH cũng cần quan tâm thêm đến các phương sai sai số của các giai đoạn trước đó nhằm biểu thị chính xác hơn sự biến đổi của các phương sai sai số, đây chính là mô hình tổng quát của mô hình ARCH thông qua mô hình GARCH. Hiệu quả của mô hình GARCH được đánh giá cao trong các dự báo kinh tế và tài chính.

Giả sử mô hình hồi quy với dữ liệu bảng tổng quát có dạng:

Trong đó: N số là đơn vị chéo (theo không gian được xếp trên các dòng) và T là số thời đoạn (được xếp trên cột) trong bảng dữ liệu; y là biến phụ thuộc, m là hệ số chặn, xit là một vectơ dòng của các biến giải thích có k phần tử, β là một vectơ có cấp là k×1 của các hệ số, uit là sai số ngẫu nhiên, và ϕ là tham số AR(1), tự hồi quy bậc 1. Với các giả định |ϕ|<1 và T đủ lớn để thỏa mãn tính nhất quán ước lượng LS.

Trong trường hợp xem xét mức biến động s_it dưới dạng mô hình GARCH (p,q) như sau:

Đối với dữ liệu bảng, nghiên cứu này xem xét vai trò của sự khác biệt giữa các biến thông qua cách đặt biến giả (dummy). Do đó, sẽ tiến hành kiểm tra sự hiện diện của các hiệu ứng riêng lẻ trong phương trình trung bình. Tiếp theo, sẽ kiểm tra các vi phạm của mô hình hồi quy dựa vào phương pháp bình phương cực tiểu OLS của mô hình có gắn với biến giả dưới dạng kiểm định phần dư (LSDV) như là kiểm tra hiệu ứng ARCH. Sau đó, nghiên cứu tiếp tục kiểm tra các hiệu ứng riêng lẻ trong quy trình phương sai điều kiện. Cuối cùng, nhóm tác giả chọn ra mô hình tốt nhất trong ước lượng mô hình phù hợp nhất với dữ liệu để đảm bảo không xảy ra hiện tượng phương sai sai số thay đổi có điều kiện.

Ứng dụng mô hình GARCH với dữ liệu kinh tế vĩ mô

Khi xem xét sự phát triển của một yếu tố kinh tế - xã hội nào đó, các nhà nghiên cứu thường phải xem xét sự biến đổi của yếu tố đó theo thời gian đồng thời sự tương tác của yếu tố đó với các yếu tố khác ở trong cùng một thời điểm. Chỉ khi đặt vấn đề nghiên cứu vào bối cảnh chung của thời điểm cũng như sự vận động riêng của chính yếu tố đó mới giúp các nhà nghiên cứu có cái nhìn toàn cảnh, có các phân tích thực sự phù hợp và đưa ra các quyết định tối ưu nhất. Vì ý nghĩa quan trọng này, họ thường phải xem xét vấn đề nghiên cứu trong tương quan về thời gian và không gian dưới dạng dữ liệu bảng.

Nghiên cứu này ứng dụng bộ dữ liệu GARCH bảng đối với bộ dữ liệu kinh tế vĩ mô của sáu quốc gia châu Mỹ Latinh gồm Argentina, Canada, Peru, Ecuador, Colombia và Uruguay trong giai đoạn từ năm 2005 đến năm 2015. Dữ liệu vĩ mô được đưa vào nghiên cứu được  World Bank cung cấp gồm: GDP, tổng vốn (K) và lao động (L) theo năm trong khoảng thời gian 10 năm (từ năm 2005 đến năm 2015).

Nghiên cứu này tập trung vào sáu quốc gia được khá nhiều người biết tới khi nhắc tới khu vực châu Mỹ Latinh, trong đó mỗi quốc gia có các đặc trưng riêng biệt để xem xét mô hình vĩ mô khi áp dụng cho các quốc gia này có sự khác biệt nhau hay không. Cụ thể, Argentina là nền kinh tế lớn thứ ba Mỹ Latinh, có xếp hạng cao về Chỉ số phát triển con người. Argentina có GDP danh nghĩa cao thứ năm và cao nhất về sức mua tương đương nên có tiềm năng rất lớn cho sự phát triển trong tương lai ở khu vực này. Trong khi đó, Canada có nền kinh tế rất phát triển và đứng vào nhóm hàng đầu thế giới. Kinh tế Canada dựa chủ yếu vào nguồn tài nguyên tự nhiên phong phú và hệ thống thương mại phát triển cao. Peru là một quốc gia đang phát triển nhưng cũng có chỉ số phát triển con người ở mức cao. Ecuador có nguồn tài nguyên dầu mỏ đáng kể và sở hữu nhiều vùng đất canh tác màu mỡ, nên xuất khẩu chủ yếu là các sản phẩm như dầu mỏ, chuối, hòa và tôm, sự biến động giá trên thị trường thế giới có ảnh hưởng lớn tới nền kinh tế trong nước. Colombia là nước giàu khoáng sản và năng lượng, nhưng sự phát triển kinh tế cũng có những giai đoạn tăng trưởng bền vững rồi giảm phát. Cuối cùng, Uruguay là nền kinh tế chủ yếu dựa vào thương mại, đặc biệt là xuất khẩu nông sản, khiến cho trong nước dễ bị biến động giá cả hàng hóa.

Với các dữ liệu đầu vào của mỗi quốc gia theo từng năm gồm: Tốc độ tăng trưởng kinh tế quốc nội (GDP), tổng vốn (K) và lao động (L), đầu tiên, nghiên cứu xem xét tính dừng của Dữ liệu bảng thông qua Bảng 1.

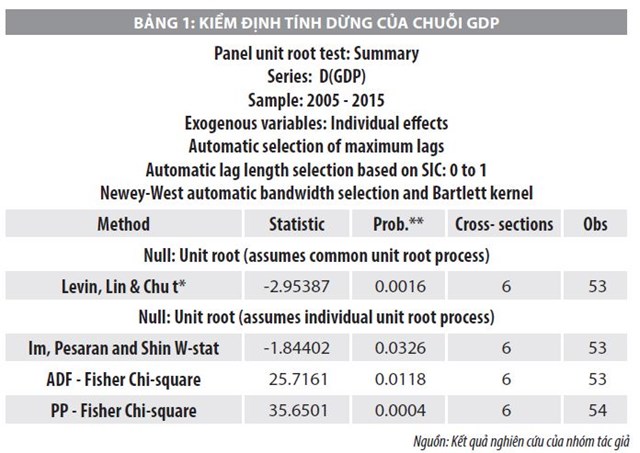
Dựa vào kết quả Bảng 1, có thể nhận thấy chuỗi GDP dừng ở sai phân bậc 1 và có ảnh hưởng của tác động riêng lẻ. Tương tự, tiến hành cho chuỗi K và L, chuỗi K cũng dừng ở sai phân bậc 1, còn chuỗi L dừng ở sai phân bậc 2, trường hợp không có tác động riêng lẻ của hằng số và xu thế. Nhóm tác giả tiếp tục xem xét giản đồ tự tương quan nhằm xem xét các bậc của mô hình tự hồi quy trung bình trượt ARIMA theo Bảng 2.

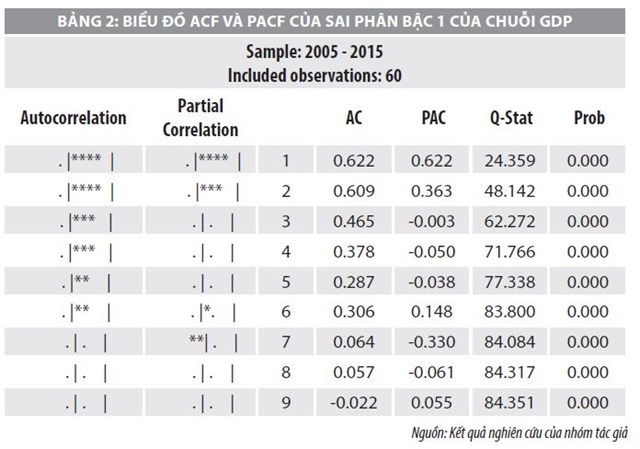
Thông qua Bảng 2 có thể thấy, các hệ số tự tương quan khác 0 một cách có ý nghĩa tương ứng với tự hồi quy các bậc là AR(1), AR(2), AR(6), AR(7), trung bình trượt đến MA(1) đến MA(6). Nghiên cứu này ước lượng các mô hình LSDV của phương trình trung bình với tác động cố định của tất cả các biến giả cũng như các biến tự hồi quy và trung bình trượt. Kết qua lựa chọn được mô hình tốt nhất có ý nghĩa thống kê với các hệ số tự hồi quy và trung bình trượt được biểu diễn qua kết quả Bảng 3.

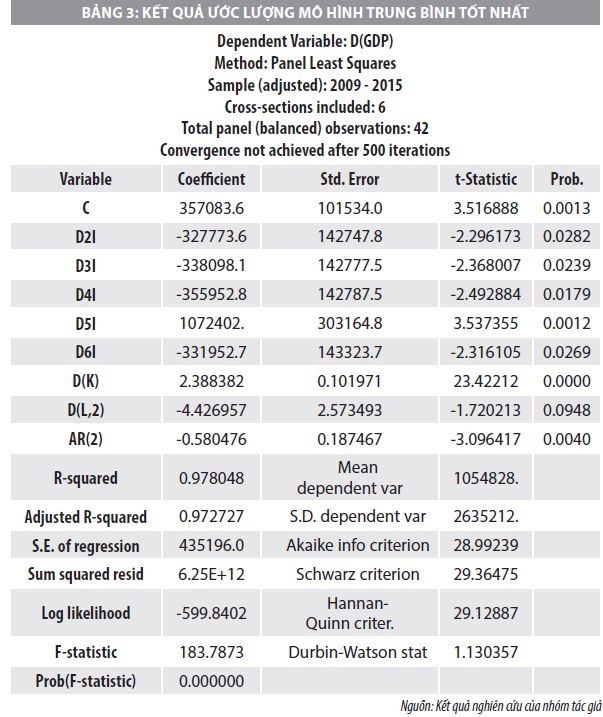
Tuy nhiên, để kiểm tra tính không đồng nhất thông qua các hiệu ứng riêng lẻ trong cả hai phương trình trung bình có điều kiện và phương trình phương sai có điều kiện, nhóm tác giả thực hiện kiểm định giả thuyết đồng thời thông qua kiểm định Wald với  H₀: m₂ = ...m₆.

Kết quả kiểm định hiệu ứng riêng lẻ mô hình trung bình, kết quả nghiên cứu được thể hiện ở Bảng 4 như sau:

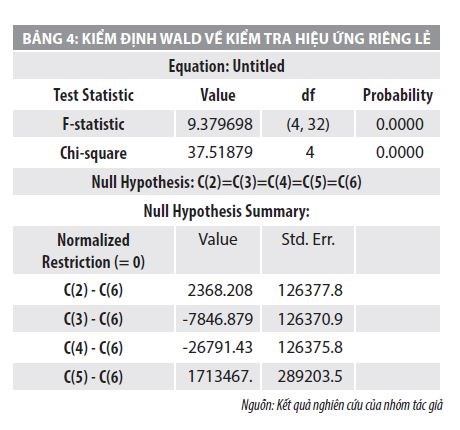
Kết quả của thống kê với giá trị kiểm định là χ²=37.51879, đủ cao để bác bỏ hoàn toàn giả thuyết H₀. Điều đó chứng tỏ không có tác động riêng lẻ trong phương trình trung bình.  Tiếp theo, nhóm nghiên cứu kiểm tra hiệu ứng ARCH của các bình phương của phần dư trong mô hình LSDV. Kết quả về hệ số tự tương quan riêng phần của phần dư bình phương được thể hiện trong Bảng 5.

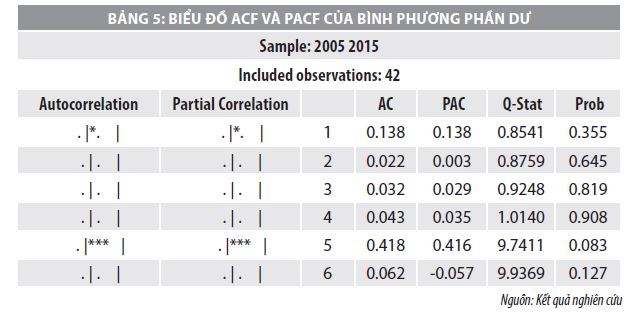
Trong Bảng 5, chỉ có hệ số tự tương quan ở độ trễ thứ 5 là có ý nghĩa thống kê ở mức 10%. Do đó, có thể phương sai có điều kiện của phần dư tuân theo ARCH (5). Thực hiện hồi quy phần dư bình phương của mô hình trung bình theo GARCH(1,1), để cho ra kết quả theo Bảng 6.

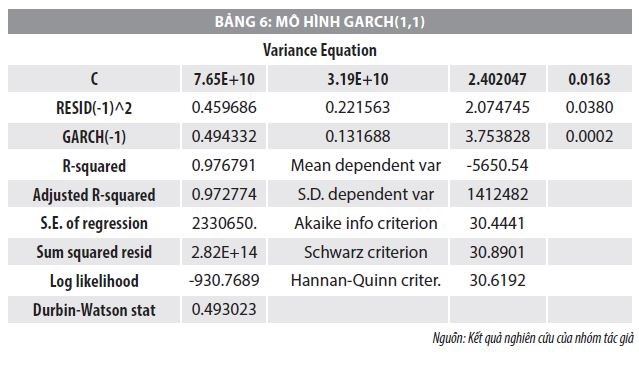
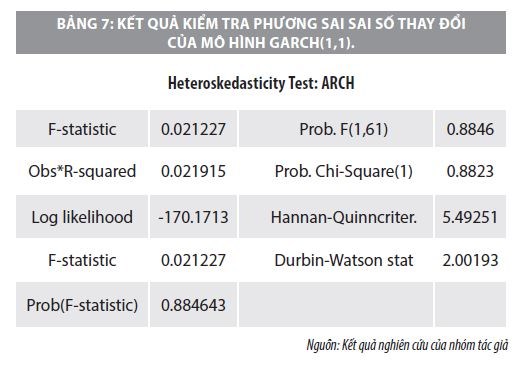
Kết quả của Bảng 6 cho thấy tất cả các hệ số của mô hình GARCH(1,1) đều có ý nghĩa thống kê ở mức 5%. Do đó, nhóm nghiên cứu tiến hành kiểm tra thêm kết quả về phương sai sai số thay đổi trong mô hình GARCH (1,1). Kết quả của kiểm tra được thể hiện trong Bảng 7.

Kết quả cho thấy, trong mô hình GARCH(1,1) đã là mô hình không còn phương sai sai số thay đổi, hoàn toàn có thể sử dụng được trong ước lượng mô hình phù hợp với dữ liệu quá khứ cũng như dự báo các giá trị trong tương lai.

Kết luận

Kết quả nghiên cứu này đã làm rõ các bước kiểm định và ước lượng mô hình GARCH cho dữ liệu bảng, ứng dụng thực nghiệm trên bộ dữ liệu bảng về GDP của 6 quốc gia châu Mỹ Latinh trong cả phương trình trung bình có điều kiện lẫn phương trình phương sai có điều kiện. Đây là một vấn đề có ý nghĩa quan trọng trong bối cảnh hầu hết các nghiên cứu thực nghiệm trước đây đều bỏ qua sự phụ thuộc giữa các quốc gia bằng cách sử dụng phương pháp đơn biến theo từng quốc gia.

Thông qua kết quả thực nghiệm về phương sai thời gian có điều kiện đặt ra sự cần thiết phải bao gồm sự phụ thuộc theo không gian trong một mô hình bảng. Phát hiện này làm cho phương pháp GARCH với dữ liệu bảng trở nên cần thiết, độc đáo và phù hợp. Đây là một đóng góp quan trọng của nghiên cứu này trong việc mở rộng mô hình GARCH truyền thống sang GARCH bảng cũng như quy trình các bước ước lượng mô hình GARCH bảng. Đồng thời, sẽ là cơ sở để mở rộng thêm nghiên cứu mô hình GARCH bảng dựa trên các biến tương tác, xem xét sự phụ thuộc giữa các biến thông qua các công cụ hiện đại như Copula, các mô hình hồi quy cập nhật thông tin theo hướng tiếp cận của thống kê Bayes.

Nói cách khác, thông qua các kết quả nghiên cứu, nhóm tác giả chỉ ra có mối quan hệ chặt giữa các nhân tố, trong đó sai phân của GDP phụ thuộc vào sai phân GDP của giai đoạn trước đó, sai phân của vốn và sai phân bậc hai của lao động, đồng thời phụ thuộc vào từng quốc gia riêng lẻ. Như vậy, khi áp dụng kết quả nghiên cứu này vào tình hình thực tiễn của Việt Nam, có thể giúp dự báo GDP trong giai đoạn tới thông qua sự tăng/giảm các dữ liệu lịch sử. Đặc biệt hơn, việc dự báo xu hướng của GDP còn tính đến các đặc điểm, yếu tố riêng có của nền kinh tế, con người Việt Nam (lao động cần cù, sáng tạo...), đồng thời đặt trong bối cảnh mới là ảnh hưởng của Cách mạng công nghiệp 4.0.

* Nghiên cứu này là sản phẩm của đề tài cấp cơ sở được tài trợ bởi trường Đại học Kinh tế - Luật, Đại học Quốc gia TP. Hồ Chí Minh với mã số CS/2018-06.         

Tài liệu tham khảo:

Baltagi, B. H. (2006). Panel data econometrics: Theoretical contributions and empirical applications. Emerald Group Publishing;

Bollerslev, T. (1986), Generalized autoregressive conditional heteroskedasticity. Journal of econometrics, 31(3), 307-327;

Box, G. E., Jenkins, G. M., Reinsel, G. C., & Ljung, G. M. (2015), Time series analysis: forecasting and control. John Wiley & Sons;

Cermeño, R., & Grier, K. B. (2006), Conditional heteroskedasticity and cross-sectional dependence in panel data: an empirical study of inflation uncertainty in the G7 countries. Contributions to Economic Analysis, 274, 259-277;

Chong, C. W., Ahmad, M. I., & Abdullah, M. Y. (1999), Performance of GARCH models in forecasting stock market volatility. Journal of forecasting, 18(5), 333-343;

Coffie, W. (2017), Conditional Heteroscedasticity and Stock Market Returns: Empirical Evidence from Morocco and BVRM. Journal of Applied Business and Economics, 19(5), 43-57;

Engle, R. (2002), Dynamic conditional correlation: A simple class of multivariate generalized autoregressive conditional heteroskedasticity models. Journal of Business & Economic Statistics, 20(3), 339-350;

Evans, T., & McMillan, D. G. (2007), Volatility forecasts: The role of asymmetric and long-memory dynamics and regional evidence. Applied Financial Economics, 17(17), 1421-1430;

Franses, P. H., & Van Dijk, D. (1996). Forecasting stock market volatility using (non‐linear) Garch models, Journal of Forecasting, 15(3), 229-235;

Pesaran, M. H. (2007), A simple panel unit root test in the presence of cross‐section dependence. Journal of applied econometrics, 22(2), 265-312;

Tsay, R. S. (2005), Analysis of financial time series (Vol. 543). John wiley & sons.