Đặt vấn đề

TFP là chỉ tiêu đo lường năng suất của đồng thời cả “lao động” và “vốn” trong một hoạt động cụ thể hay cho cả nền kinh tế. TFP phản ảnh sự tiến bộ của khoa học, kỹ thuật và công nghệ, qua đó sự gia tăng đầu ra không chỉ phụ thuộc vào tăng thêm về số lượng của đầu vào, mà còn tùy thuộc vào chất lượng của các yếu tố đầu vào, đó là lao động và vốn. Cùng với lượng đầu vào như nhau, lượng đầu ra có thể lớn hơn nhờ vào việc cải tiến chất lượng của lao động, vốn và sử dụng có hiệu quả các nguồn lực này.

TFP được tính từ phương pháp ước lượng nguồn tăng trưởng từ hàm sản xuất. Sau khi trừ đi các yếu tố đóng góp về lượng (lao động và vốn) cho tăng trưởng, phần còn lại của tăng trưởng là do đóng góp về sự gia tăng hiệu quả của nền kinh tế, gọi là TFP. Hệ số này càng cao chứng tỏ nền kinh tế càng hiệu quả và ngược lại…

Nguồn gốc phân tích TFP trong nền kinh tế bắt đầu từ bài nghiên cứu của Solow (1957), tuy nhiên, những năm gần đây đã chứng kiến bước phát triển trong các nghiên cứu cả lý thuyết lẫn thực nghiệm về TFP. Bước tiến này được thúc đẩy nhờ sự phát triển mạnh mẽ của các công cụ tin học, sự hoàn thiện về phương pháp luận trong ước lượng TFP từ giữa những năm 1990 (Ackerberg và các cộng sự, 2007) và sự sẵn có ngày càng tăng của các dữ liệu cấp doanh nghiệp (DN), cho phép ước lượng TFP ở cấp độ DN.

Thông thường các nghiên cứu năng suất cấp độ DN, giả thiết đầu ra (được đo bằng lượng bán hoặc giá trị gia tăng đã loại trừ yếu tố lạm phát) là một hàm của các đầu vào của DN (Katayama và các cộng sự, 2009). Độ đo TFP thu được như là phần dư trong quan hệ hàm số này khi đó được sử dụng để đánh giá tác động của các biện pháp chính sách khác nhau như mức sở hữu nước ngoài (Javorcik, 2004). Van Beveren, I. (2007, 2012) đã có tổng quan rất tốt các nghiên cứu về ước lượng TFP.

Trên thực tế đã có một số ước lượng thực nghiệm được đề xuất, đáp ứng những đòi hỏi lý thuyết này, trong nghiên cứu này nhóm tác giả lựa chọn hai vấn đề nổi lên là: Thứ nhất, chú ý ở các ước lượng bán tham số vì nhiều nghiên cứu thực nghiệm trước đây dựa vào các kỹ thuật ước lượng này. Thứ hai, đề cập thuật toán ước lượng: (i) Thuật toán ước lượng bán tham số của Olley và Pakes - OP (1996); (ii) Thuật toán ước lượng bán tham số của Levinsohn, Petrin (2003); (iii) Thuật toán của Ackerberg-Caves-Frazer (2006); (iv) Thuật toán của Wooldrige (2009).

Mục thực nghiệm của nghiên cứu này sẽ sử dụng dữ liệu các DN chế tác Việt Nam để minh họa các ước lượng và phân rã coi như thử nghiệm so sánh đánh giá tác động của chính sách đến đóng góp của việc cải thiện năng suất bên trong DN hay sự phân bổ lại nguồn. Các phần tiếp theo sẽ cung cấp các vấn đề phương pháp luận nảy sinh khi ước lượng TFP cấp độ DN; Điểm qua một số phương pháp ước lượng và minh họa các phương pháp luận khác nhau đối với ngành chế tác của Việt Nam, đồng thời đưa ra một số kết luận.

Các vấn đề phương pháp luận

Hàm sản xuất

Nghiên cứu bắt đầu bằng việc giả thiết rằng sản xuất có dạng hàm sản xuất Cobb-Douglas. Cụ thể, hàm sản xuất dạng như sau:

 (1)

Trong đó: Yit là đầu ra hiện vật của DN i trong thời kỳ t; Kit, Lit và Mit tương ứng là các đầu vào về vốn, lao động và đầu vào trung gian và Ait là mức hiệu quả trung tính Hick của DN i trong thời kỳ t. Giả thiết các nhà kinh tế lượng quan sát được Y_it, K_it, L_it và M_it (mặc dù thường dưới dạng giá trị chứ không phải lượng), Ait không quan sát được đối với nhà kinh tế lượng. Lấy loga tự nhiên của (1) dẫn đến một hàm sản xuất tuyến tính theo loga:

y_it = β₀ + β_kk_it + β_ll_it + β_mm_it + β_it

Trong đó, các chữ thường chỉ logarit tự nhiên và  ln(A_it) = β₀ + ε_it

β₀ đo mức hiệu quả trung bình giữa các DN và qua thời gian; ε_it là độ lệch riêng theo thời gian và nhà sản xuất so với trung bình đó, mà sau đó có thể được phân rã thêm thành phần có thể quan sát được (ít nhất là có thể dự đoán) và thành phần không thể quan sát được. Điều này dẫn đến phương trình sau:

  (2)

Đặt ω_it = β₀ + v_it biểu thị năng suất cấp độ DN và  là một thành phần i.i.d. (có phân phối độc lập, đồng nhất), biểu thị các độ lệch không dự báo so với trung bình do sai số đo, những trễ không dự báo hoặc các hoàn cảnh bên ngoài khác.

Điển hình, các nhà nghiên cứu thực nghiệm ước lượng (2) và giải ra đối với ωit. Năng suất ước lượng khi đó có thể được tính toán như sau:

(3)

Mức năng suất có thể thu được như là hàm mũ của , nghĩa là . Độ đo năng suất là kết quả của phương trình (3) có thể được sử dụng để đánh giá ảnh hưởng và tác động của các biến chính sách khác nhau trực tiếp ở cấp độ DN; hoặc một cách khác, TFP cấp độ DN có thể được gộp về cấp độ ngành bằng cách tính toán trung bình có trọng số theo tỷ lệ đóng góp của các .

Các trọng số được sử dụng để gộp TFP cấp độ DN có thể hoặc là các tỷ lệ đóng góp trong đầu ra cấp độ DN (trong OP); hoặc là các tỷ lệ đóng góp về việc làm (trong De Loecker và Konings, 2006). Điều này sẽ được chỉ ra trong phần thực nghiệm, năng suất ngành chuẩn hóa, sau đó có thể được phân rã thêm thành một trung bình không trọng số và một số hạng hiệp phương sai mẫu. Mặc dù những khác nhau trong các trung bình không trọng số qua thời gian thể hiện những thay đổi bên trong DN từ TFP, những thay đổi trong số hạng hiệp phương sai mẫu báo hiệu sự phân bổ lại thị phần như một lực đẩy của dịch chuyển năng suất (Olley và Pakes, 1996; De Loecker và Konings, 2006).

Ước lượng năng suất nhân tố tổng hợp

Có thể sử dụng các thuật toán sau: (i) Thuật toán ước lượng Olley-Pakes (1996); (ii) Thuật toán ước lượng Levinsohn-Petrin là các tuật toán giải quyết chệch do sự lựa chọn ngành; (iii) Thuật toán Ackerberg-Caves-Frazer (ACF, 2006) mở rộng ước lượng bán tham số của OP để giải quyết các vấn đề đa cộng tuyến và nhận diện với biến lao động.

Cụ thể, (ACF, 2006) gợi ý một thủ tục ước lượng, trong đó hệ số đối với lao động (trong hàm sản xuất giá trị gia tăng) không được ước lượng trong giai đoạn thứ nhất của thuật toán ước lượng nữa. Tất cả các hệ số của đầu vào thu được trong giai đoạn thứ hai, còn giai đoạn thứ nhất chỉ dùng để làm ròng thành phần sai số trong hàm sản xuất. Hệ số của lao động được nhận diện trong giai đoạn thứ hai bằng cách áp dụng Phương pháp bình phương bé nhất phi tuyến (NLLS) hoặc phương pháp momen tổng quát (GMM), tùy thuộc vào các giả thiết về thời gian đối với biến lao động. Nếu lao động được giả thiết là được quyết định trước khi hiện thực hóa năng suất, có thể áp dụng NLLS.

Mặt khác, nếu lao động được giả thiết là tương quan với năng suất, cần áp dụng ước lượng GMM trong giai đoạn thứ hai. (ACF, 2006) chỉ ra thêm rằng, thủ tục ước lượng hoàn toàn phù hợp với những hàm ý động gắn với phân bổ lao động. Trong trường hợp này, ước lượng LP có điều chỉnh là ước lượng được ưa thích hơn, vì động thái của lao động có thể tác động lên lựa chọn cả vốn lẫn lao động hiện thời, nhưng không tác động lên những lựa chọn đầu vào trung gian của các DN.                                                                      

Áp dụng thực nghiệm vào ngành công nghiệp chế tác Việt Nam

Nghiên cứu này sẽ minh họa một số phương pháp luận khác nhau với việc sử dụng dữ liệu cấp độ DN đối với ngành chế tác Việt Nam. Bộ dữ liệu sử dụng trong nghiên cứu này là số liệu hỗn hợp dựa trên điều tra DN hàng năm của Tổng cục Thống kê từ năm 2000 đến năm 2016 của các DN ngành công nghiệp chế tác. Đầu ra và các biến tính bằng tiền của các DN đều được điều chỉnh theo chỉ số giảm phát năm gốc là năm 2000. Biến lao động (L) tính bằng đơn vị người thể hiện bằng số công nhân có việc làm trong năm. Số liệu về lượng vốn (K), đầu ra, đầu vào trung gian (M) và giá trị gia tăng (VA), doanh thu (R) được tính bằng đơn vị triệu đồng.

Kết quả các hệ số của hàm sản xuất

Bảng 1 trình bày các hệ số của hàm sản xuất thu được sử dụng các phương pháp luận khác nhau.

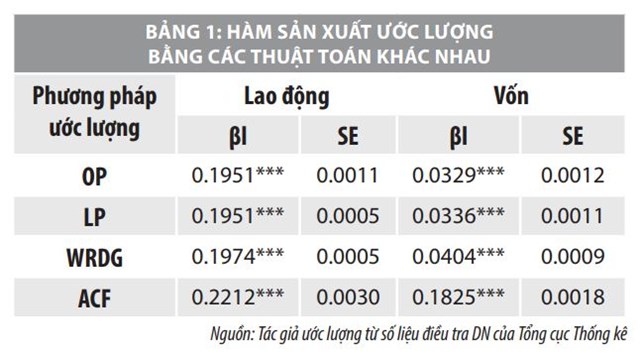
Kết quả ước lượng cho thấy, hệ số của “lao động” trong 2 phương pháp OP và LP là như nhau, chỉ khác nhau rất nhỏ ở sai số tiêu chuẩn của ước lượng. Tuy nhiên, hệ số của “vốn” ước lượng từ LP cao hơn ước lượng từ OP một chút (0.0336 - 0.0329).

Vì ước lượng GMM về mặt lý thuyết có thể hiệu chỉnh đối với chệch do tính đồng thời, β_l  trong dòng 3 của Bảng 3 được cả hệ số của “vốn” và “lao động” đều nhỉnh hơn hệ số của “vốn” và “lao động” ước lượng từ OP và LP. Tuy nhiên, hệ số của lao động ước lượng từ GMM lại cao hơn hệ số lao động ước lượng từ ACF, trong khi đó thì hệ số của “vốn” ước lượng bằng phương pháp GMM lại thấp hơn hệ số của “vốn” ước lượng từ ACF.

Các hệ số hàm sản xuất thu được trong Bảng 3 có thể được sử dụng để tính toán năng suất cấp độ DN đối với mỗi năm trong mẫu. Bằng việc áp dụng tính ổn định của hệ số lên mô hình, có thể giữ lại toàn bộ mẫu các DN đối với tất cả các ước lượng, ngay cả khi không có đầu tư dương (như đối với các ước lượng OP). Trên cơ sở phương trình (3) ta thu được năng suất cấp độ DN đối với các ước lượng OP, LP, ACF và GMM.

Phân rã Olley-Pakes năng suất gộp

Cuối cùng, sử dụng các ước lượng của năng suất cấp độ DN thu được từ việc áp dụng phương trình (3) vào mẫu sử dụng các hệ số hàm sản xuất từ Bảng 3, có thể tính toán năng suất gộp ngành đối với mỗi năm trong mẫu như một trung bình có trọng số của TFP cấp độ DN:

Φ_jt=∑_i□s_ijtΩ_ijt         (4)

Ở đây sit là một trọng số riêng biệt theo DN, bằng  (s_it/(∑_is_it)) và s biểu thị hoặc doanh thu hoặc số việc làm (De Loecker và Konings, 2006). Chuẩn hóa chỉ số này về 1 vào năm 1996 cho phép ta so sánh sự tiến hóa của TFP gộp trong ngành Chế tác đối với các ước lượng khác nhau đã thảo luận ở đây.

Để đánh giá sự tiến triển của TFP gộp trong ngành công nghiệp thực phẩm và đồ uống là do những cải thiện trong TFP ở cấp độ DN hay là do sự phân bổ lại thị phần giữa các DN, có thể sử dụng các phân rã khác nhau (De Loecker và Konings, 2006). Ta sẽ dựa vào phân rã Olley và Pakes (1996), phân rã năng suất gộp thành thành phần bên trong và một số hạng covariance theo cách sau đây:

                        (5)

Ở đây (Ω_t) là trung bình không trọng số của TFP cấp độ nhà máy và là hiệp phương sai mẫu giữa TFP và các tỷ lệ đóng góp đầu ra (hoặc việc làm).

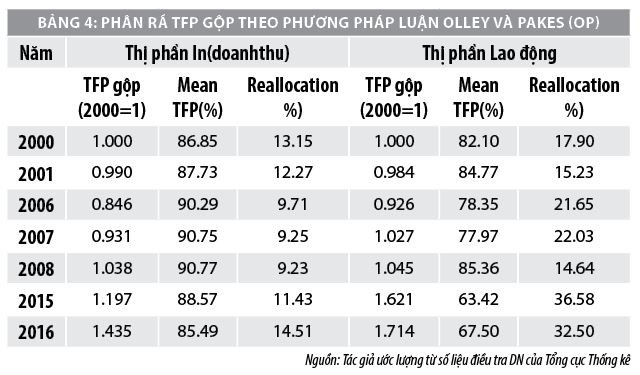
Các kết quả áp dụng phân rã này sử dụng hoặc tỷ lệ doanh thu (bên trái) hoặc tỷ lệ việc làm (bên phải) đối với độ đo TFP GMM, được trình bày trong Bảng 4. Cột thứ nhất đối với mỗi loại tỷ lệ đóng góp gồm độ đo năng suất trung bình có trọng số theo tỷ lệ đóng góp được tính toán trên cơ sở phương trình (4), chuẩn hóa về 1 đối với năm 2000. Cột thứ hai và thứ ba tương ứng chỉ ra tỷ lệ phần trăm đóng góp của thành phần năng suất bên trong và tỷ lệ phân bổ lại trong TFP có trọng số gộp.  

Sử dụng các ước lượng TFP cho các mục đích đánh giá

Kết quả ước lượng TFP từ các cách tiếp cận khác nhau

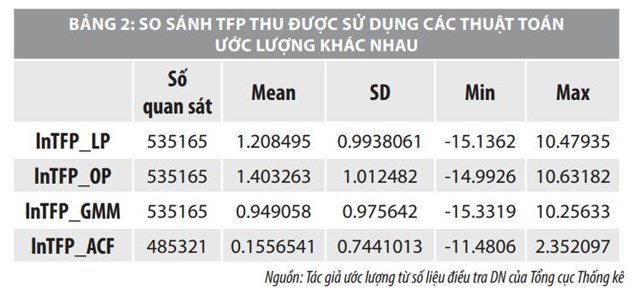
Trước hết ta trình bày kết quả ước lượng TFP từ các phương pháp khác nhau như Bảng 2.

Bảng 2 cho thấy, các ước lượng thu được của TFP từ phương phâp OP và LP không khác nhau. TFP trung bình đối với các ước lượng OP và LP là 1,208 và 1,403. Đối với ước lượng LP, TFP trung bình hơi thấp hơn so với TFP ước lượng từ OP. Uớc lượng ACF có TFP trung bình và cũng có một độ lệch chuẩn thấp nhất so với các ước lượng khác.                   

Bảng 3 cho thấy, tương quan giữa ước lượng TFP khác nhau, các độ đo TFP thu được sử dụng GMM, OP, LP và ACF tương quan rất cao (luôn cao hơn 0,84).

Kết quả phân rã Olley-Pakes của TFP từ các cách tiếp cận khác nhau

Nghiên cứu trình bày vắn tắt kết quả phân rã OP của TFP được ước lượng từ các phương pháp khác nhau như Bảng 4.

Kết quả ước lượng ở Bảng 4 chỉ ra rằng, hầu hết những cải thiện năng suất được thực hiện trong ngành chế tác từ năm 2000 là gắn với tăng trưởng năng suất bên trong DN. Khi sử dụng các tỷ lệ đóng góp việc làm chứ không phải tỷ lệ doanh thu, tỷ lệ phân bổ lại hơi lớn hơn so với trường hợp tỷ lệ đóng góp doanh thu.

Kết luận

Nghiên cứu đã điểm lại các vấn đề phương pháp luận nảy sinh khi ước lượng TFP ở cấp độ DN. Đã thảo luận các chệch truyền thống gây, do tính đồng thời của việc chọn đầu vào và tính nội sinh của lựa chọn đầu vào, cũng như một số vấn đề nổi lên gần đây hơn. Nghĩa là liên quan đến cạnh tranh không hoàn hảo trong các thị trường đầu vào và/hoặc đầu ra và tính nội sinh của lựa chọn sản phẩm.

Trong những thập kỷ qua, tăng trưởng kinh tế của Việt Nam phụ thuộc nhiều vào sự tích lũy của các yếu tố đầu vào đặc biệt là vốn đầu tư trực tiếp nước ngoài. Ngoài ra, Việt Nam vẫn tập trung tăng cường sử dụng lao động vào huy động sử dụng vốn là chủ yếu. Khi các yếu tố đầu vào sẵn có và rẻ thì chiến lược này rất phù hợp. Tuy nhiên, nền kinh tế Việt Nam hiện nay phát triển ở mức cao hơn, bên cạnh chiến lược tăng trưởng dựa vào đầu vào, thì phải định hướng vào nâng cao hiệu quả sử dụng nguồn vốn và lao động, đó chính là nâng cao TFP. Nghiên cứu thực tiễn từ ngành chế tác Việt Nam cho thấy, cần tập trung nâng cao chỉ số TFP, trong đó chú trọng sự đóng góp của các yếu tố như: Trình độ công nghệ, chất lượng lao động, công nghệ quản lý… Từ đó, góp phần nhiều hơn vào sự phát triển của DN và tăng trưởng của nền kinh tế.     

Tài liệu tham khảo:

1. Ackerberg, D.A., Caves, K. and Frazer, G. (2006), Structural identification of production functions. Unpublished manuscript;
2. Bernard, A.B., Redding, S.J. and Schott, P.K. (2009), Products and productivity. Scandinavian Journal of Economics 111(4): 681–709;
3. De Loecker, J. and Konings, J. (2006), Job reallocation and productivity growth in a post-socialist economy: evidence from Slovenian manufacturing. European Journal of Political Economy 22: 388–408;
4. Levinsohn, J. and Petrin, A. (2003), Estimating production functions using inputs to control for unobservables. Review of Economic Studies 70: 317–341.